If the r.v.s X and Y have the Bivariate Normal distribution with parameters μ 1 , μ 2 in R,0 < Ï 1 , Ï

If the r.v.s X and Y have the Bivariate Normal distribution with parameters μ₁, μ₂in R,0 < σ₁, σ₂< ˆž. and p ˆˆ [-1, 1], show that their joint ch.f. is given by

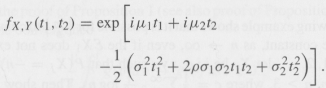
 For this purpose, do the following:

(i) Assume first that μ₁ = μ₂ = 0 and σ₁ = σ₂ = 1, and use Exercises 12 (ii) in Chapter 9 and 13 (ii) in this chapter to show that:

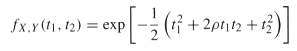
(ii) For the general case, use the transformations U = (X €“ μ₁)/σ₁, V = (Y €“ μ₂)/σ₂ and verify that ԐU = ԐV = 0, Var(U) = Var(V) = 1, p(U, V) = p(X, Y) = p. Then use Exercise 15 in Chapter 9 and part (i) here to arrive at the desired expression for the ch.f. f_X.Y.

fx,Y (t1, 12) = exp iuiti +iuzt2 (oi + 2po102112 + oik)| + 2p0102t|12 +