Question: Let the r.v.s Xj, j ¥ 1, be distributed as follows: Show that the Lindeberg condition (relation (12.24)) holds, if and only if α <

Let the r.v.s Xj, j ‰¥ 1, be distributed as follows:

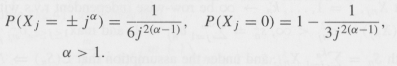
1 1 P(X; = ± jª) = a > 1. P(X; =0) = 1 – 6j2(a-1)' %3D 3 j2(a-1) '

Show that the Lindeberg condition (relation (12.24)) holds, if and only if α < 3/2. Conclude that

Let the r.v.s Xj, j ‰¥ 1, be distributed as

Let the r.v.s Xj, j ‰¥ 1, be distributed as

For α < 3/2, show that

Let the r.v.s Xj, j ‰¥ 1, be distributed as

which is implied by n2a < ɛ2sn2 for large n, so that gn (ɛ) = 0. Next,

gn(É›) ‰¥ 1 - É›2/18 (l €“ 1/k)(2- 1/k) k2a/É›2sn2 k3-2a,

Where k = [(É›sn)l/α], and conclude that the expression on the right-hand side does not converge to 0 for α ‰¥ 3/2.

1 1 P(X; = j) = a > 1. P(X; =0) = 1 6j2(a-1)' %3D 3 j2(a-1) '

Step by Step Solution

★★★★★

3.43 Rating (166 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

Here X j 0 2 j 2 X j X 2 j 2j 2 6j 21 13 j 2 so that s 2 n nn12n118 Consider js with j 1 ... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Document Format (1 attachment)

Word file Icon

742-M-S-P (6987).docx

120 KBs Word File

Students Have Also Explored These Related Statistics Questions!

Q:

Let X n , n ¥ 1, be independent r.v.s distributed as B (1, Ï ), and set Then show that And n- , . X,

Q:

For j = 1,2 n, let Xj be independent r.v.s defined as follows: Then show that the Lindeberg condition (condition (12.24)) does not hold. Recall that and show that, for every É > 0 and large n:...

Q:

Let Verify that for n ¥ 1, Can either inequality be used to show that S diverges? Show that and conclude that S diverges. n2n

Q:

If the independent r.v.s Xj, j ¥ 1, are distributed as U (-j, j), then show that the Lindeberg condition (see relation (12.24)) holds, so that Where Recall that X ~ U(α,...

Q:

1. A player throws a fair die and simultaneously flips a fair coin. If the coin lands heads, then she wins twice, and if tails, then one-half of the value that appears on the die. Determine her...

Q:

can someone solve this Modern workstations typically have memory systems that incorporate two or three levels of caching. Explain why they are designed like this. [4 marks] In order to investigate...

Q:

# 5: Fourier Interpolant and DFT 1 The Discrete Fourier Transform (DFT) of a periodic array fj , for j = 0, 1, . . . , N 1 (corresponding to data at equally spaced points, starting at the left end...

Q:

# 5: Fourier Interpolant and DFT 1 The Discrete Fourier Transform (DFT) of a periodic array fj , for j = 0, 1, . . . , N 1 (corresponding to data at equally spaced points, starting at the left end...

Q:

\fCHAPTER 14 Server Farms: M/M/k and M/M/k/k In today's high-volume world, almost no websites, compute centers, or call centers consist of just a single server. Instead a \"server farm\" is used. The...

Q:

2 STAT 330: Mathematical Statistics Winter 2016 Assignment 2 Name: ID: Due on Feb 29th (Monday) 11:30am in drop boxes across the hall from MC 4065/4066. 1 1. [7 marks] Let f (x, y) = kxy 2 , if 0 x...

Q:

In a paper of approximately 2,400 words, review the theories developed to explain male criminal behavior and discuss why they are inadequate to explain delinquency in females. How have these beliefs...

Q:

Theorem EIM says that if is an eigenvalue of the nonsingular matrix A, then 1 is an eigenvalue of A-1. Write an alternate proof of this theorem using the characteristic polynomial and without...

Q:

In Japan, commercial banks can own a company's stock up to: Multiple Choice Commercial banks cannot own stocks of companies. 1 % of the total shares. 1 0 % of the total shares. 5 % of the total...

Q:

What does the standard deviation tell about a data set? A. How diverse the population is. B. The mean of the population as it relates to the median. C. The specification limits of the population. D....

Q:

Merck & Co. conducted a study to test the promise of its experimental AIDS vaccine ( The Boston Globe , September 22, 2007). Volunteers in the study were all free of the human immunodeficiency virus...

Q:

More and more households are struggling to pay utility bills given a shaky economy and high heating costs (The Wall Street Journal, February 14, 2008). Particularly hard hit are households with homes...

Q:

The research team at a leading perfume company is trying to test the market for its newly introduced perfume. In particular the team wishes to look for gender and international differences in the...

Q:

Steve and Kelly own a single - family home insured under an Insurance Services Office ( ISO ) Homeowners 3 Special Form ( HO - 3 ) policy. One evening, a fire destroys the home s living room and...

Q:

As discussed in class, riding circuit on horseback is the historical term that led to the current name for these courts: Multiple Choice State trial courts State supreme courts Federal appellate...

Q:

Body Header Styles Go to the sf effects.css file in your editor. Within the Body Header Styles section, create a style rule for the body element to add drop shadows to the left and right border of...