Question: Let (X, Y,Z) be the position of an object's CM, and let (x, y, z) be the position relative to the CM. Prove the parallel-axis

Let (X, Y,Z) be the position of an object's CM, and let (x, y, z) be the position relative to the CM. Prove the parallel-axis theorem, equation. (8.17), by setting x = X + x, y = Y + y, and z = Z + z in equation.(8.8).

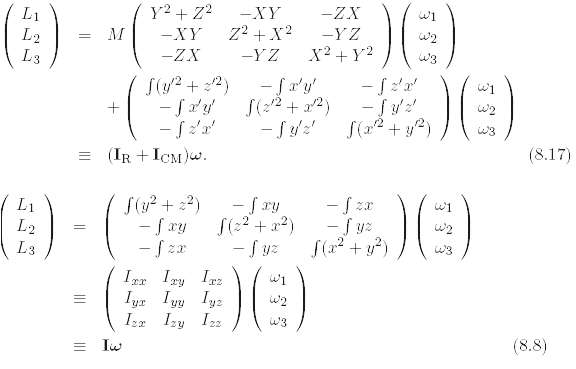
Y2 + Z2 L1 L2 L3 -ZX -XY w1 Z2 + X?

Y2 + Z2 L1 L2 L3 -ZX -XY w1 Z2 + X? -XY -YZ X2 + Y2 -ZX -YZ w3 - S'y' S(:2 + a2) - Sy/2' S(? + ) - fa'y - fr' = (IR + ICM)w. - Sy2 S(22 + y2) (8.17) (E) S(1? + 22) - f ry - f zx - fyz S(? + y?) -fry S(22 +x2) L1 w1 L2 L3 Iyx Iny Iz Iyr Iyy Iyz Iz Izy Izz w3 = Iw (8.8)

Step by Step Solution

★★★★★

3.32 Rating (161 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Consider one of the diagonal entries in I say I11 f y 2 In terms of the new variables this equals ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Document Format (1 attachment)

36-P-M-A-M (202).docx

120 KBs Word File

Students Have Also Explored These Related Mechanics Questions!

c. Calculate the rate of return of the price-weighted index for the second period ( t = 1 to t = 2). Consider the three stocks in the following table. Pt represents price at time t, and Qt represents...

The instantaneous position of an object is specified by its position vector r leading from a fixed origin to the location of the point object. Suppose that for a certain object the position vector is...

The position of an object undergoing simple harmonic motion is given by x = A cos(Bt). Explain the physical significance of the constants A and B. What is the frequency of this object's motion?

Math 1172 Project #1 Applications of Integration Due: Tuesday, September 12 Name(s): - - - - - - - - - - - - - - - - - - - - Description - - - - - - - - - - - - - - - - - - - The definite integral is...

Let A, B be sets. Define: (a) the Cartesian product (A B) (b) the set of relations R between A and B (c) the identity relation A on the set A [3 marks] Suppose S, T are relations between A and B, and...

1. A player throws a fair die and simultaneously flips a fair coin. If the coin lands heads, then she wins twice, and if tails, then one-half of the value that appears on the die. Determine her...

Briefly describe ASCII and Unicode and draw attention to any relationship between them. [3 marks] (b) Briefly explain what a Reader is in the context of reading characters from data. [3 marks] A...

(a) In SystemVerilog, what is the difference between: (i) The ternary operator ? and if...then...else statements? [2 marks] (ii) always_ff and always_comb? [2 marks] (iii) Blocking, non-blocking and...

watch the three short clips below then answer the questions Copy and paste the three links below 1) Projectile Motion https://www.nsf.govews/mmg/mmg_disp.jsp?med_id=72205&from= 2) Newton's Second Law...

MA 261 PRACTICE PROBLEMS 1. If the line ` has symmetric equations y x1 z+2 2 = 3 = 7 , nd a vector equation for the line `0 that contains the point (2; 1; 3) and is parallel to `. A. ~ = (1 + 2t)~...

What are postretirement benefits other than pensions?

List five Risk identification methods Explain three of the listed techniques(methods) as they are used. Explain four basic types of Risk response Give examples of one each that can be used for...

Think about the attractions and activities of your last holiday was it a predominantly romantic or collective gaze that influenced your experience? Were your activities characterized by the gaze, or...

The following payroll liability accounts are included in the ledger of Harmon Company on January 1, 2022. FICA Taxes Payable .......................................$ 760.00 Federal Income Taxes...

Change each of the following percents into a common fraction in lowest terms. 3/5%

Explain the concept of rational expectations.

What are the effects of an increase in credit market risk on aggregate economic activity? How does this matter for the current financial crisis?

Given a linear program in slack form such that the basic solution is feasible, give an algorithm to find a vertex of the feasible region by optimizing the slack form.

Explain the challenges faced in the use of SSL accelerators.

A rectangular beam with semicircular notches, as shown in part (b) of the figure, has dimensions h = 0.88 in. and h1 = 0.80 in. The maximum allowable bending stress in the metal beam is max = 60ksi,...

A rectangular beam with semicircular notches, as shown in part (b) of the figure, has dimension h = 120mm and h1 = 100mm. The maximum allowable bending stress in the plastic beam is max = 6MPa, and...

A rectangular beam with notches and a hole (see figure) has dimensions h = 5.5in., h1 = 5in., and width b = 1.6in. The beam is subjected to a bending moment M = 130k-in., and the maximum allowable...

Dillon Labs has asked its financial manager to measure the cost of each specific type of capital as well as the weighted average cost of capital. The weighted average cost is to be measured by using...

Say your income is $ 1 0 0 K . Given the following tax brackets, what is your effective tax rate? Taxrate Taxable Income ( Single ) . 1 0 % 1 2 % $ 1 1 , 0 0 1 to $ 4 4 , 7 2 5 $ 4 4 , 7 2 6 to $ 9 5...

You own a portfolio that has 2,920 shares of stock A, which is priced at $17.50 per share and has an expected return of 10.11%, and 2,786 shares of stock B, which is priced at $9.00 per share and has...