Let X 1 , brvbar , X n be independent identically distributed (i i d ) r v s defined on the probability space (W, A , P ) and having d f F Let F n be empirical d f defined in terms of the Xi s i e , Then show that is a r v That is, although D n ( Atilde ) is arrived at through non countable operations, it is still a r v Define Fn(x, w) number of X1( ), , X( ) x ,

Question: Let X 1 ,¦, X n be independent identically distributed (i.i.d.) r.v.s defined on the probability space (W, A , P ) and having d.f.

LetX₁,€¦,X_nbe independent identically distributed (i.i.d.) r.v.s defined on the probability space (W,A,P) and having d.f.F. LetF_nbe empirical d.f. defined in terms of theXis; i.e.,

Fn(x, w) = -[number of X1(@), ..., X„(@) < x], п

Then show that

Let X1,..., Xn be independent identically distributed (i.i.d.) r.v.s defined

is a r.v. That is, although D_n(Ã—) is arrived at through non-countable operations, it is still a r.v.

Define

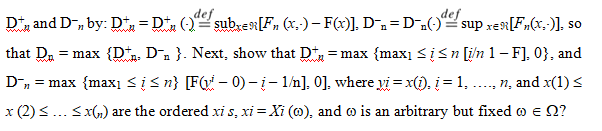
Let X1,..., Xn be independent identically distributed (i.i.d.) r.v.s defined

Fn(x, w) = -[number of X1(@), ..., X(@) < x],

Step by Step Solution

★★★★★

3.44 Rating (180 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Consider the quantities D n D n D n and y i i 1 n mentioned in the hint ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Document Format (1 attachment)

742-M-S-P (6948).docx

120 KBs Word File

Students Have Also Explored These Related Statistics Questions!

For n = 1, 2,¦., let X n , Y n and X , Y be r.v.s defined on the probability space (W, A , P ), and suppose that Where r, s > 1 with 1/ r + 1/ s = 1. Then show that ( , Y Xn 00 00

For n ³ 1, let X n , Y n , and X be r.v.s defined on the probability space (W, A, P), and suppose that As n ¥. Then, as n¥: (i) A constant, implies (ii) Implies , 4

For n = 1, 2,¦, suppose that X n and X are r.v.s defined on the probability space (W, A , P ), and suppose that And { X n } are uniformly integrable. Then show that Uniformly in A Ã A ....

If Xn, n 1, are i.i.d. r.v.s defined on the probability space (, A, P), then (i) Show that the process X = (X1, X2, ...) is ergodic. (ii) Derive the Strong Law of Large Numbers under the assumption...

Problem 2 (5 points). For n N, let X1, ..., X, be independent identically distributed random variables on some discrete probability space (Q, A, P). Suppose E[X]

MATH S350 TMA 01 Hints Question 1 Let A and B be the event that water is contaminated with excessive amount of pollutant A and pollutatnt B respectively. Remarks: 1. Half of those communities whose...

Answer TURE or FALSE for these six questions and explain reason simply. 1. Let A, B be events defined in a common probability space. Suppose that P(A) 1. Then, Var (X) > Var (Y). 3. Let {Xx}, k = 1,...

Problem 1. Problem 2. Problem 3. Problem 4. 1. (10 points) Let X; for i =1,2,..., n be independent and identically distributed random variables with mean u > 0 and standard deviation o > 0. When we...

please may i have help with both parts of 3) (3) Let {X} be a sequence of independent and identically distributed uniform on (0,1) random variables. Let 0 *}. (a) Show that: P(N(x) > *) - [2 marks]...

Let X1, X2, X3 be independent and identically distributed (i.i.d) random variables with the probability mass function (pmf) is f (x) = (1 - p)-p, x = 1,2,3 ... 0, otherwise, where p = -. That is, X1,...

Write chemical equations expressing each of the following: (a) Preparation of o-nitrophenyl acetate by sulfuric acid catalysis of the reaction between a phenol and a carboxylic acid anhydride. (b)...

Find the photon energy for light of wavelength (a) 450 nm, (b) 550 nm, (c) 650 nm.

Inventory Valuation under Variable Costing Refer to the data for Genelia Company. During the most recent year, Genelia Company had the following data associated with the product it makes: Units in...

You are managing the installation of a new oil well pump in a very productive well. Due to very efficient management and significant personal effort, the project is completed several days ahead of...

According to the January theory, if the stock market is up for the month of January, it will be up for the year. If it is down in January, it will be down for the year. According to an article in The...

Suppose the National Hurricane Center forecasts that hurricanes will hit the strike area with a .95 probability. a. What probability distribution does this follow? b. If there are 10 hurricanes this...

A recent CBS News survey reported that 67% of adults felt the U.S. Treasury should continue making pennies. Suppose we select a sample of 15 adults. a. How many of the 15 would we expect to indicate...

Dozier Corporation is a fast-growing supplier of office products. Analysts project the following free cash flows (FCFs) during the next 3 years, after which FCF is expected to grow at a constant 9%...

(Ignore income taxes in this problem.) Chow Company has gathered the following data on a proposed investment project: Investment required in equipment $142,500 Annual cash inflows $30,000 Salvage...

Carlson Products, a constant growth company, has a current stock price of $20.00. Carlson's next dividend, D1, is forecasted to be $2.00, and is expected to grow at an annual rate of 6%. Carlson has...