Show that Sup{| F n ( x , Ï) F ( x )|; x R1} For 0 < p < 1, define x p by:

Show that

Sup{|F_n(x, ω) €“ F(x)|; x ˆˆ R1}

For 0 < p < 1, define x_p by: x_p = inf{x ˆˆ R; F(x) ‰¥ p}, so that F(x) ‰¥ p for x ‰¥ x_p, and F(x) < p for x < x_p, which implies F(x_p €“ 0) ‰¤ p. Next, replace p by i/k (k ‰¥ 2 integer), i = 0, 1,€¦, k, to get the points xki, with €“ ˆž ‰¤ xko < xk1, and xk,k€“1 < xkk ‰¤ ˆž. Then, for x ˆˆ [i/k, i+1/k), i = 0, 1,€¦., k €“ 1, it holds that

i/k ‰¤ F (xki) ‰¤ F(x) ‰¤ F (x_k,i+1€“0) ‰¤ i + 1/k.

so that F(xk,i+1€“ 0) €“ F(xki) ‰¤ 1/k. Use this result and the non-decreasing property of the F and F_n to obtain, for x ˆˆ R and i = 0, 1,€¦., k:

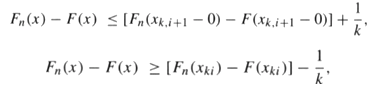
So that

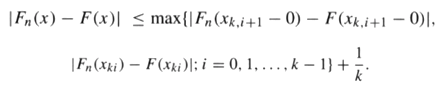
Finally, take the sup over x ˆˆ R (which leaves the right-hand side intact), and use the SLLN to each one of the (finitely many) terms on the right-hand side to arrive at the asserted conclusion?

a.s. 0.