Linear algebraic equations can arise in the solution of differential equations. For example, the following differential equation derives from a heat balance for a long, thin rod (Figure):?

d²T/dx² + h? (T_? ? T) = 0

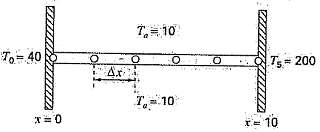
Where T = temperature (^oC), x = distance along the rod (m), h? = a heat transfer coefficient between the rod and the ambient air (m ^?2), and T_? = the temperature of the surrounding air (^oC). This equation can be transformed into a set of linear algebraic equations by using a finite divided difference approximation for the second derivative (recall Section 4.1.3),

d²T/dx² = T_i+₁ ? 2T_i + T_i-1/?x²

where T_i designates the temperature at node i. This approximation can be substituted into Eq. (P12.38) to give

-T_i-1 + (2 + h? ?x²)T_i ? T_i+1 = h? ?x² T_u

This equation can be written for each of the interior nodes of the rod resulting in a tridiagonal system of equations. The first and last nodes at the rods ends are fixed by boundary conditions.

(a) Develop an analytical solution for Eq. (P12.38) for a 10-m rod with T_u = 20, T(x = 0) = 40, T(x = 10) = 200 and h? = 0.02.

(b) Develop a numerical solution for the same parameter values employed in (a) using a finite-difference solution with four interior nodes as shown in Figure. (?x = 2 m).

T,= 10 To= 40 T= 200 T= 10 r= 10