Consider two vibrations of equal amplitude and frequency but differing in phase, one along the x-axis, x = a sin (wt - a) and the other along the y-axis, y = a sin (wt - ?) These can be written as follows:(a) Multiply Eq. (1) by sin ? and Eq. (2) by sin a, and then subtract the resulting equations.(b) Multiply Eq. (1) by cos ? and Eq. (2) by cos a, and then subtract the resulting equations.(c) Square and add the results of parts (a) and (b).(d) Derive the equation x2 + y2 ?? 2xy cos ? = a2 sin2 ?, where ? = a ?? ?.(e) Use the above result to justify each of the diagrams in Fig.33.61 (next page). In the figure, the angle given is the phase difference between two simple harmonic motions of the same frequency and amplitude, one horizontal (along the x-axis) and the other vertical (along the y-axis). The figure thus shows the resultant motion from the superposition of the two perpendicular harmonic motions.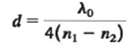

d= 4(n = m2)