This problem involves the use of crosscorrelation to detect a signal in noise and estimate the time delay in the signal. A signal x(n) consists of a pulsed sinusoid corrupted by a stationary zero-mean white noise sequence. That is,

x(n) = y(n – n₀) + ω(n)            0 ≤ n ≤ N – 1 

where ω(n) is the noise with variance σ²_ω and the signal is

y(n) = A cosω₀n,         0 ≤ n ≤ N – 1

        = 0,                  otherwise

The frequency ω₀ is known but the delay n₀, which is a positive integer, is unknown, and is to be determine by crosscorrelating x(n) with y(n). Assume that N > M + n₀. Let 

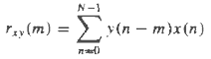
Denote the crosscorrelation sequence between x(n) and y(n). in the absence of noise this function exhibits a peak at delay m = n₀. Thus n₀ is determined with no error. The presence of noise can lead to errors in determining the unknown delay.

(a) For m = n₀, determine E[r_xy(n₀)]. Also, determine the variance, var[r_xy(n₀)], due to the presence of the noise. In both calculations, assume that the double frequency term averages to zero. That is, M » 2π/ω₀.

(b) Determine the signal-to-noise ratio, defined as

SNR = {E[r_xy(n₀)]}2 / var[r_xy(n₀)]

(c) What is the effect of the pulse duration M on the SNR?

N-1 (m) %3D - )x ()