Question: Prove these. (a) For any is an additive inverse of then is an additive inverse of. So a vector is an additive inverse of any

Prove these.

(a) For any 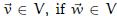v E is an additive inverse of  then is an additive inverse of. So a vector is an additive inverse of any additive inverse of itself.

(b) Vector addition left-cancels: if 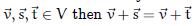 implies that

v E

Step by Step Solution

★★★★★

3.39 Rating (158 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

a Let V be a vector space let and assume that is an ad... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Document Format (1 attachment)

Word file Icon

961-M-L-A-L-S (5180).docx

120 KBs Word File

Students Have Also Explored These Related Linear Algebra Questions!

Q:

In a vector space every element has an additive inverse. Can some elements have two or more?

Q:

Prove each, assuming that the operations are defined, where G, H, and J are matrices, where Z is the zero matrix, and where r and s are scalars. (a) Matrix addition is commutative G + H = H + G. (b)...

Q:

An additive to interior house paint has been recently developed that may greatly increase the ability of the paint to resist staining. An investigation was conducted to determine whether the additive...

Q:

\fCOMPLEX VARIABLES AND APPLICATIONS Eighth Edition James Ward Brown Professor of Mathematics The University of Michigan-Dearborn Ruel V. Churchill Late Professor of Mathematics The University of...

Q:

\fCOMPLEX VARIABLES AND APPLICATIONS Eighth Edition James Ward Brown Professor of Mathematics The University of Michigan-Dearborn Ruel V. Churchill Late Professor of Mathematics The University of...

Q:

Midterm 1. Are the expressions p q and q p logically equivalent? Use a truth table to prove your answer. 2. Determine whether the following propositions are true or false: a. 5 is an odd number and 3...

Q:

Ryan Ren Math4A-02-S17-Williams WeBWorK assignment number Week6 is due : 05/15/2017 at 06:01am PDT. The Gauchospace link for the course contains the syllabus, grading policy and other information....

Q:

I've attached what I have thus far and then the notes that I received back below the questions. I need to prove A1 - A10. Some require specific numeric entries. I attempted this but need to more...

Q:

need correction options, with reason, Only, QUESTION 5 Let V be the set of all 3x3 matrices with Real number entries, with the usual definitions of scalar multiplication and vector addition. Consider...

Q:

ASSUMPTIONS A set, R , with two operations, + and *, is a ring if the following properties are shown to be true: 1. Closure property of addition: for all s and t in R , s + t is also in R 2. Closure...

Q:

The catering manager of LaVista Hotel, Lisa Ferguson, is disturbed by the amount of silverware she is losing every week. Last Friday night, when her crew tried to set up for a banquet for 500 people,...

Q:

In a normal distribution the probability of a value between 2 and 3 standard deviations below the mean is? -2.35% .15% -.15% 2.35%

Q:

Yellow Tang fish most likely originated in the A . Federated States of Micronesia B . Hawaiian Islands C . Johnston Atoll D . Northern Mariana Islands

Q:

Use the following graph of the market for cigarettes to answer the questions: a. According to the graph, how much is the government tax on cigarettes?

Q:

For the matrix A in Exercise 34, use the CayleyHamilton Theorem to compute A3 and A4 by expressing each as a linear combination of I, A, and A2.

Q:

For the matrix A in Exercise 33, use the CayleyHamilton Theorem to compute A-1 and A-2 by expressing each as a linear combination of I and A. In exercise 33 An important theorem in advanced linear...

Q:

For the matrix A in Exercise 34, use the Cayley-Hamilton Theorem to compute A - 1 and A -2 by expressing each as a linear combination of I, A, and A2.

Q:

Question 5 of 12 (1 point) Attempt 1 of 1 |View question in a popup @1h 49m Remaining 6.2 Section Monthly Mortgage Payments The average monthly mortgage payment including principal and interest is...

Q:

J&R Renovation, Inc., is trying to determine its cost of debt. The firm has a debt issue outstanding with 14 years to maturity that is quoted at 105 percent of face value. The issue makes semiannual...

Q:

ABC Boat Corporation has pulled off a miraculous recovery. Ten years ago, it was near bankruptcy. Now the firm has just announced a $ 4 per share dividend for the next year, the first since the...