Reference Points, Happiness and Envy: The stylized results from the happiness literature suggest that happiness, at least as reported on surveys, is “reference-based” in the sense that people evaluate how happy they are not exclusively based on how much they have but, at least in part, based on how much they have relative to everyone else in their proximity.

A: This form of reference-based tastes differs from what we encounter in other settings in the sense that the “reference point” is typically something internal to the individual—such as the individual’s current endowment.

(a) Explain how one might interpret the combination of the two empirical claims cited in the text as evidence of such reference-basted determinants of happiness. (The two empirical claims are: (1) within countries, happiness is increasing with income; and (2), excluding countries and times of extreme poverty, there appear to be little relationship between average happiness and average income across countries or across time.)

(b) Suppose we have a situation where we have to allocate a fixed amount of money between two individuals. Individual 1 has reference-based preferences, with his happiness increasing only in his own consumption but decreasing in individual 2’s consumption. Individual 2, on the other hand, has the usual preferences — with his happiness increasing only in his own consumption. In what sense is individual 1 driven in part by “envy” while individual 2 is not?

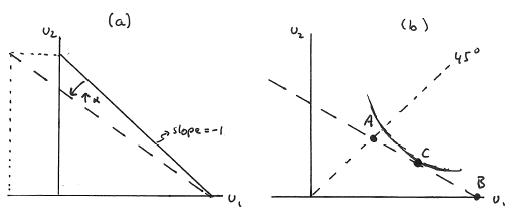
(c) Suppose utility for individual 2 is simply equal to dollars of consumption and utility for individual 1 is dollars of own consumption minus some fraction α of dollars of individual 2’s consumption. Begin by drawing the utility possibility frontier for the case where α = 0. Then show how the utility possibility frontier changes as α increase.

(d) True or False: When α = 0, equal division of resources between the two individuals is socially optimal for any social indifference map that is symmetric across the 45-degree line—including the Rawlsian, the Benthamite and any that fall in between these extremes.

(e) Now consider the utility possibility frontier when α > 0. How will the Rawlsian and Benthamite social indifference maps now give different optimal divisions of resources? What about in between social indifference maps that are symmetric across the 45 degree line?

Graph 29.4: Social Welfare and Envy

(f) For an equal allocation of utilities when α > 0, will resources also be equally allocated? (g) True or False: Envy is rewarded by each of our social indifference maps — but increasingly more rewarded as we move from the Rawlsian to the Benthamite extreme.

(h) Can you explain how many might feel discomfort in incorporating such reference-based preferences as a foundation for normative analysis of redistribution?                                                

B: Let x indicate individual 1’s consumption (in dollars) and let y indicate individual 2’s consumption (in dollars). Suppose that individual 1’s utility is given by u₁(x, y) = x −αy and individual 2’s utility is given by u₂(x, y) = y −βx.

(a) If the overall level of consumption to be divided between these two individuals is I, set up the maximization problem that maximizes individual 2’s utility subject to individual 1 attaining utility u1 and subject to the overall resource constraint.

(b) Solve for the allocation (x, y) as a function of u1 — i.e. solve for the optimal allocation of I between the two individuals given that individual 1 gets utility u1. (Hint: You do not need to solve your optimization problem from (a) — because the two constraints by themselves determine the solution to the problem.)

(c) Solve for the utility possibility frontier u₂ (u₁, I)—i.e. a function giving the utility individual 2 can get as a function of u₁ and I (as well as the α and β parameters).

(d) Consider the special case in which α = 0.5 and β = 0. Which of the two individuals now has reference-based preferences—and in what way can you characterize these as being driven by some degree of “envy”.

(e) What allocation of utilities and resources will be chosen if the ethical standard determining the distribution of resources is encompassed in the Benthamite social welfare function W = u1 +u2? Does the same division of resources hold for any combination of α > β?

(f) Repeat (for the case of α = 0.5 and β = 0) using the Cobb-Douglas social welfare function W = u₁^0.5 u₂⁰.5and then using the Rawlsian social welfare function W =min {u₁, u₂}.

(g) Does your conclusion from A (g) hold?

Transcribed Image Text:

く6 ) 2. slope-l