Question: A second-order system has a single zero: For a step input, show that: (a) y(t) can exhibit an extremum (maximum or minimum value) in the

A second-order system has a single zero:

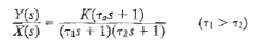
K(ras + 1) X(s) (7as + 1)(725 +1) Y(s) (T1 > 12)

For a step input, show that:

(a) y(t) can exhibit an extremum (maximum or minimum value) in the step response only if

image

(b) Overshoot occurs only for ?0/?1.

(c) Inverse response occurs only for ?a (d) If an extremum in y exists, the time at which it occurs can be found analytically. What is it?

(d) If an extremum in y exists, the time at which it occurs can be found analytically. What is it?

K(ras + 1) X(s) (7as + 1)(725 +1) Y(s) (T1 > 12)

Step by Step Solution

★★★★★

3.42 Rating (165 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

From Eq 615 a Extremum y t 0 b Over... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Document Format (1 attachment)

Word file Icon

38-E-C-E-P-C (86).docx

120 KBs Word File

Students Have Also Explored These Related Chemical Engineering Questions!

Q:

Show that the inverse A1 exists if and only if none of the eigenvalues 1, , n of A is zero, and then A1 has the eigenvalues 1/ 1, , 1/n.

Q:

Show that a matrix B has a left inverse if and only if BT has a right inverse.

Q:

If each cord can sustain a maximum tension of T before it fails, determine the greatest weight of the flowerpot the cords can support. Given: T = 50 N θ1 = 30 deg θ2 = 30 deg θ3 =...

Q:

A vertical force P is applied to the ends of cord AB of length a and spring AC. If the spring has an unstretched length δ, determine the angle θ for equilibrium. Given: P = 10 lb δ...

Q:

The following transactions apply to Jova Company for 2018, the first year of operation: 1. Issued $10,000 of common stock for cash. 2. Recognized $210,000 of service revenue earned on account. 3....

Q:

Refer to Problem 14-42. How would your answer change if instead the trust were a complex trust that makes no distributions in 2012 and 2013? Assume the trust earns $8,000 of corporate bond interest...

Q:

=+50. U.S. unemployment rate 2013, part 2. Using the data from Exercise 49 develop and compare the following models:

Q:

1. On February 1, 2010, Pat Weaver Inc. (PWI) issued 10%, $1,000,000 bonds for $1,116,000. PWI retired all of these bonds on January 1, 2011, at 102. Unamortized bond premium on that date was...

Q:

can you solve the below: Year 2 0 1 0 2 0 1 1 2 0 1 2 2 0 1 3 2 0 1 4 2 0 1 5 Stock A ( % ) - 1 1 1 1 1 - 4 5 7 Stock B ( % ) 2 5 1 3 1 8 - 6 - 3 3 1 - : a . Average return and volatility for each...

Q:

The Auto Company of America (ACA) produces four types of cars: subcompact, compact, intermediate, and luxury. ACA also produces trucks and vans. Vendor capacities limit total production capacity to...

Q:

If you had the two enantiomers of carvone in unmarked bottles, could you use just your nose and a polarimeter to determine? (a) Whether it is the (+) or (-) enantiomer that smells like spearmint? (b)...

Q:

Productivity gains have fueled the expansion of American business over the last 30 years including through several jobless recoveries. A) What are the only two ways to increase productivity?

Q:

Describe how control charts are drawn and used to determine if a process is out of statistical control. Explain the International Standards for quality documentation. Introduction Developing...

Q:

Select two or three of their attributes that Elon Muskshould either immolate or avoid in professional life. Define, cite, and apply these traits. Provide examples from your research, cite your...

Q:

Consider a project in which you are currently involved (or in which you have recently been involved). Describe the two different types of contracts that is available for you to use, and which one...

Q:

you should draft a description of the project ((project name Marketing for the Clubs Hubspot))and an initial write up of your stakeholders - identify the stakeholders. For each stakeholder and/or...

Q:

1. 8. What if the Trust Game were played in reverse? Gary first decides whether to cooperate (Gary gets $15, Jen gets $15) or defect (Gary gets $30, Jen gets $0). Jen then decides whether to accept...

Q:

On October 1, 2021, Adoll Company acquired 2,600 shares of its $1 par value stock for $38 per share and held these shares in treasury. On March 1, 2023, Adoll resold all the treasury shares for $34...

Q:

About 15 technicians were responsible for the maintenance of machinery. At any one time, one machine would be set aside for maintenance work. Ninety percent of the time, a machine that was designated...

Q:

Using the failure rate data in Table 10.1, evaluate the reliability and mean time between failures for the high-pressure interlock in Fig. 10.4. Assume that the failure rate for the solenoid switch...

Q:

Consider the liquid storage tank with a low-level inter-lock, as shown in Fig. 10.4. Suppose that an independent low-level alarm is added, with its set-point value above the value for the low-level...

Q:

Repeat Exercise 10.7 for the case where the flow meters are triply redundant; that is, there are three identical flow meters with two in the backup mode. How much would the overall system reliability...

Q:

Eamed Income Credit, Child and Dependent Care Credit (LO 7.2, 7.3) Clarita is a single taxpayer that lives in the U.S. with two dependent children, ages 10 and 12 . Clarito pays $3,000 in qualified...

Q:

For this PROGRAM you will calculate the coefficient of lift for a given flight - path angle based on wind tunnel data stored in a file.

Q:

Compute and evaluate the standard financial ratios - see Ratios tab. Add at least one or more per category of your choosing that is significant to your healthcare system Compute and evaluate the...