Slow transverse flow around a cylinder (see Fig. 3.7-1). An incompressible Newtonian fluid approaches a stationary cylinder with a uniform, steady velocity v_∞ in the positive x direction. When the equations of change are solved for creeping flow, the following expressions⁵ are found for the pressure and velocity in the immediate vicinity of the cylinder (they are not valid at large distances): Here p_∞ is the pressure far from the cylinder at y = 0 and with the Reynolds number defined as Re = 2Rv_∞p/μ. 

(a) Use these results to get the pressure p, the shear stress τ_rθ, and the normal stress τ_rr at the surface of the cylinder. 

(b) Show that the x-component of the force per unit area exerted by the liquid on the cylinder is 

(c) Obtain the force F₁, = 2CπLμv_∞ exerted in the x direction on a length L of the cylinder.   

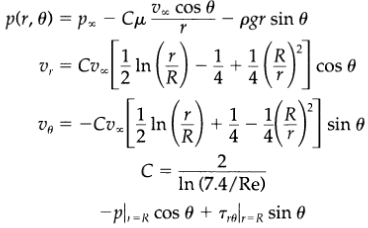
V% Cos 0 p(r, 0) = pz Cu Pgr sin 0 v, = Cv In cos 0 4 1(! 1 R Va = -Cv. In sin 0 4 C = In (7.4/Re) -pl, -R Cos 0 + T,olr=R sin 0