Velocity distribution for creeping flow toward a slot (Fig. 3B.7) it is desired to get the velocity distribution given for the upstream region in the previous problem. We postulate that v_θ = 0, v_z = 0, v, = v_r (r = θ), and P = P(r, θ).

(a) Show that the equation of continuity in cylindrical coordinates gives v, = f(θ)/r, where f(θ) is a function of θ for which df/dθ = 0 at θ = 0, and f = 0 at θ = π/2. 

(b) Write the r- and θ-components of the creeping flow equation of motion, and insert the expression for f(θ) from (a). 

(c) Differentiate the r-component of the equation of motion with respect to θ and the θ-component with respect to r. Show that this leads to 

(d) Solve this differential equation and obtain an expression for f(θ) containing three integration constants. 

(e) Evaluate the integration constants by using the two boundary conditions in (a) and the fact that the total massflow rate through any cylindrical surface must equal w. This gives 

(f) Next from the equations of motion in (b) obtain P(r, θ) as what is the physical meaning of P_∞? 

(g) Show that the total normal stress exerted on the solid surface at 0 = π/2 is 

(h) Next evaluate to on the same solid surface. 

(i) Show that the velocity profile obtained in Eq. 3B.8-2 is the equivalent to Eqs. 3B.7-2 and 3

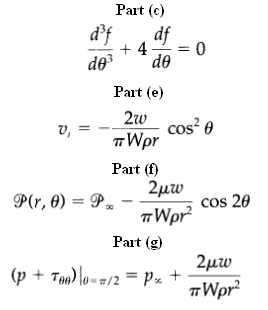
Part (c) df df + 4 de de Part (e) cos 0 v, Wpr Part (f) 2 P(r, 0) = P - cos 20 TWpr Part (g) 2 (p + Tom) lo-=/2 = Px + TWpr?