Let G be Z₃₆ . Refer to the proof of Theorem 35.11. Let the subnormal series (1) be {0} < (12) < (3) < Z₃₆ and let the subnormal series (2) be {0} < (18) < Z₃₆. Find chains (3) and (4) and exhibit the isomorphic factor groups as described in the proof. Write chains (3) and (4) in the rectangular array shown in the text.

Data from Theorem 35.11

Two subnormal (normal) series of a group G have isomorphic refinements. Proof Let G be a group and let {e} =H₀< H₁ < H₂ < · · · < H_n = G and {e} = K₀ < K₁ < K₂ <· · ·  < k_m = G be two subnormal series for G. For i where 0 ≤  i ≤ n - 1, form the chain of groups H_i = H_i(H_i+1 ∩ K0) ≤ H_i(H_i+1 ∩ K₁) ≤ · · · ≤ H_i(H_i+1 ∩ K_m)= H_i+1.This inserts m -1 not necessarily distinct groups between H_i and H_i+1. If we do this for each i where 0 ≤ i ≤ n - 1 and let H_ij = H_i(H_i+1 ∩ K_j), then we obtain the chain of groups 

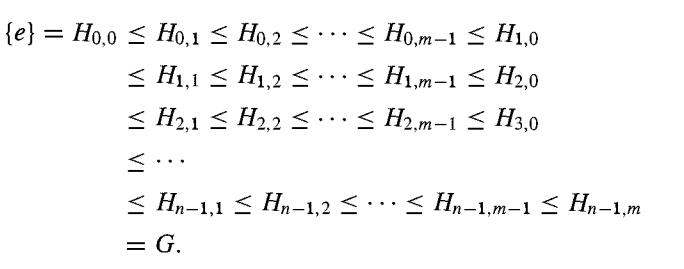
This chain (3) contains nm + 1 not necessarily distinct groups, and H_i,0 = H_i for each i. By the Zassenhaus lemma, chain (3) is a subnormal chain, that is, each group is normal in the following group. This chain refines the series (1). In a symmetric fashion, we set K_j,i = K_j(K_j+1 ∩ H_i) for 0 ≤ j ≤ m - 1 and 0 ≤ i ≤ n. This gives a subnormal chain

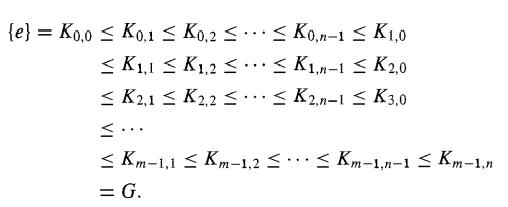
This chain ( 4) contains mn + 1 not necessarily distinct groups, and K_j,0 = K_j for each j. This chain refines the series (2). By the Zassenhaus lemma 35 .10, we have H_i(H_i+1 ∩ K_j+1) H_i(H_i+1 ∩ K_j) ≈ K_j(K_j+1 ∩ H_i+1)/K_j(k_j+1 ∩ H_i), or H_i,j+1/H_i,j ≈ K_j,i+1/K_j,i for 0 ≤ i ≤ n - 1 and 0 ≤ j ≤ m - 1. The isomorphisms of relation (5) give a one to-one correspondence of isomorphic factor groups between the subnormal chains (3) and (4). To verify this correspondence, note that H_i,0 = H_i and H_i,m = H_i+1, while K_j,0 = K_j and K_j,n = K_j+1· Each chain in (3) and (4) contains a rectangular array of mn symbols ≤. Each ≤ gives rise to a factor group. The factor groups arising from the rth row of ≤'s in chain (3) correspond to the factor groups arising from the rth column of ≤'s in chain (4). Deleting repeated groups from the chains in (3) and (4), we obtain subnormal series of distinct groups that are isomorphic refinements of chains (1) and (2). This establishes the theorem for subnormal series. 

For normal series, where all H_i and K_j are normal in G, we merely observe that all the groups H_i,j and K_j,i formed above are also normal in G, so the same proof applies. This normality of H_i,j and K_j,i follows at once from the second assertion in Lemma 34.4 and from the fact that intersections of normal subgroups of a group yield normal subgroups.

Transcribed Image Text:

{e}= H0,0 ≤ H0,1 ≤ H0,2 ≤ < Ho,m− < H1,0 ≤ H₁,1 ≤ H1,2 ≤... ≤ H1,m-1 ≤ H2,0 ≤ H2,1 ≤ H2,2 ≤...