Let X be a simplicial complex. For an (oriented) n-simplex of X, the coboundary n () of is the (n + 1)

Let X be a simplicial complex. For an (oriented) n-simplex σ of X, the coboundary δⁿ(σ) of σ is the (n + 1) chain ∑τ, where the sum is taken over all (n + 1)-simplexes τ that have σ as a face. That is, the simplexes τ appearing in the sum are precisely those that have σ as a summand of ∂_{n+ 1} (τ). Orientation is important here. Thus P₂ is a face of P₁P₂, but P₁ is not. However, P₁ is a face of P₂P₁. Let X be the simplicial complex consisting of the solid tetrahedron of Fig. 41.2. 

a. Compute δ⁽⁰⁾(P₁) and , δ⁽⁰⁾(P₄). 

b. Compute ,δ⁽¹⁾(P₃P₂). 

c. Compute δ⁽²⁾(P₃P₂P₄).

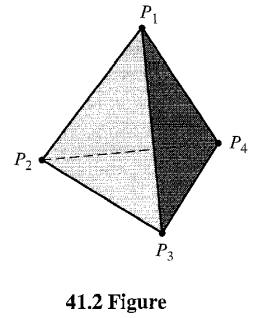
P2 P P3 41.2 Figure P4