With reference to Exercise 10, the torus X can be mapped onto its circle b (which is homeomorphic to S¹) by a variety of maps. For each such map f : X → b given below, describe the homomorphism f_*n : H_n(X) → H_n(b) for n = 0, 1, and 2, by describing the image of generators of H_n(X) as in Exercise 10. 

a. f: X → b given by f((θ, ∅)) = (θ, 0)

b. f: X → b given by  f((0, ∅)) = (2θ, 0)

Data from Exercises 10

Every point P on a regular torus X can be described by means of two angles θ and ∅, as shown in Fig. 43.16. That is, we can associate coordinates (θ, ∅) with P. For each of the mappings f of the torus X onto itself given below, describe the induced map f_*n of H_n(X) into H_n(X) for n = 0, 1, and 2, by finding the images of the generators for H_n(X) described in Example 42.12. Interpret these group homomorphisms geometrically as we did in Example 43.9. 

Data from Figure 43.16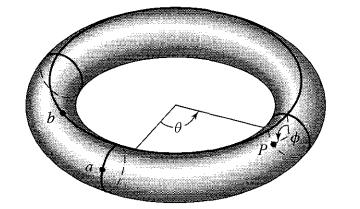

0% PER b