The join E v L of two extension fields E and L of F in F̅ is the smallest subfield of F̅ containing both E
and L. That is, E v L is the intersection of all subfields of F̅ containing both E and L. Let K be a finite normal
extension of a field F, and let E and L be extensions of F contained in K as shown in Fig. 53.10. Describe
G(K/(E v L)) in terms of G(K/E) and G(K/L).

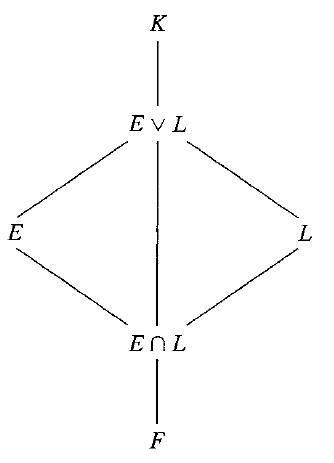
E K EVL ENL F L