We consider the field E = Q(√2, √3, √5). It can be shown that [E : Q] = 8. In the notation of Theorem 48.3, we have the following conjugation isomorphisms (which are here automorphisms of E):

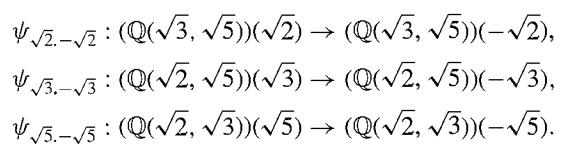
For shorter notation, let τ₂ = ψ√_2.-√2, τ₃ = ψ_{√3 -√3}, and , τ₅ = ψ_√5.-√5· Compute the indicated element of E.

Data from Theorem 48.3

Let F be a field, and let α and β be algebraic over F with deg(α, F) = n. The map ψ_α.β :F(α) → F(β) defined by ψ_α.β(c₀+ciα +· · ·+ C_n-1α^n-¹) = c₀ + c₁β + · · ·+ C_n-1β^n-1 for c_i ∈ F is an isomorphism of F(α) onto F(β) if and only if a and are conjugate over F.

Proof Suppose that ψ_α.β : F(α) → F(β) as defined in the statement of the theorem is an isomorphism. Let irr(σ, F) = a₀ + a₁x + · · · + a_nxⁿ. Then a₀ + a₁α + · · · + a_nαⁿ = 0, so ψ_α.β(a₀ + a₁α + ... + a_nαⁿ) = a₀ + a₁β + ... + a_nβⁿ = 0.

By the last assertion in the statement of Theorem 29.13 this implies that irr(β, F) divides irr(α, F). A similar argument using the isomorphism (ψ_α.β)^-1 = ψ_β,α shows that irr(α, F) divides irr(β, F). Therefore, since both polynomials are monic, irr(α, F) = irr(β, F), so α and β are conjugate over F.

Conversely, suppose irr(α, F) = irr(β, F) = p(x). Then the evaluation homomorphisms ∅_α: F[x] → F(α) and ∅_β : F[x] → F(β) both have the same kernel (p(x)). By Theorem 26.17, corresponding to ∅_α: F[x] → F(α), there is a natural isomorphism ψ_α mapping F[x]/(p(x)) onto ∅_α:[F[x]] = F(α). Similarly, ∅_β gives rise to an isomorphism ψ_β mapping F[x]/(p(x)) onto F(β). Let ψ_α.β = ψ_β(ψ_α)^-1. These mappings are diagrammed in Fig. 48.4 where the dashed lines indicate corresponding elements under the mappings. As the composition of two isomorphisms,ψ_α.β is again an isomorphism and maps F(α) onto F(β). For (c₀ + c₁α + · · + c_n-1a^n-1) ∈ F(α), we have

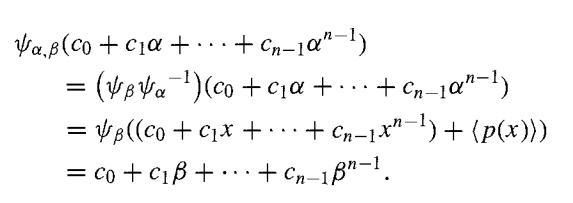
Thus ψ_α,β is the map defined in the statement of the theorem.

2.-2 : (Q(3, 5))(2) (Q(3, 5))(-2), V3.-3: (Q(2, 5))(3) (Q(2, 5))(-3), 5.-5 : (Q(2, 3))(5) (Q(2, 3))(-5).