In problem verify the foregoing result for the given matrix.

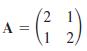
Let P denote a matrix whose columns are eigenvectors K₁, K₂, . . . , K_n corresponding to distinct eigenvalues λ₁, λ₂, . . . , λ_n of an n × n matrix A. Then it can be shown that A = PDP^-1, where D is a diagonal matrix defined by

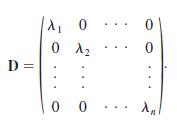
A = 1 1 2/