Question: Show that the 5 5 matrix has an eigenvalue 1 of multiplicity 5. Show that three linearly independent eigenvectors corresponding to 1

Show that the 5 × 5 matrix

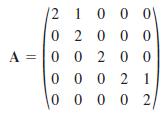
2 1 00 0' 0 2 0 0 0 A = 0 0 2 0 0 0 0 0 0 2 1 0 0 0 0 2


has an eigenvalue λ1 of multiplicity 5. Show that three linearly independent eigenvectors corresponding to λ1 can be found.

2 1 00 0' 0 2 0 0 0 A = 0 0 2 0 0 0 0 0 0 2 1 0 0 0 0 2

Step by Step Solution

★★★★★

3.48 Rating (161 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

Here we are given a 5X5 matrix Let the given matrix be A So we know that auxiliary equ... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Document Format (2 attachments)

PDF file Icon

1527_605d88e19d0ba_848765.pdf

180 KBs PDF File

Word file Icon

1527_605d88e19d0ba_848765.docx

120 KBs Word File

Students Have Also Explored These Related A First Course in Differential Equations Questions!

Q:

Consider the 5 5 matrix given in Problem 31. Solve the system ' = AX without the aid of matrix methods, but write the general solution using matrix notation. Use the general solution as a basis for...

Q:

Let A be a 4 4 real symmetric matrix with eigenvalues 1 = 1, 2 = 3 = 4 = 0 (a) Explain why the multiple eigenvalue = 0 must have three linearly independent eigenvectors x2, x3, x4. (b) Let x1 be an...

Q:

Without calculation, find one eigenvalue and two linearly independent eigenvectors of Justify your answer 22 21 A=1222 2

Q:

3. An eigenvalue for a matrix A has associated to it the algebraic multiplicity and the geometric multiplicity. Recall that the geometric multiplicity of an eigenvalue A is the largest possible...

Q:

Hello, please help me with these questions, and give explanations for the answers. Please don't use cursive as I can't read that, and please don't type the explanations. These are practice examples I...

Q:

Can you please help me with number 21. I have provided the math chapter it came from and the answer from the back of the book: Thank you so much and Best wishes! Open with Chapter 5 Linear Systems...

Q:

Given is a 3 X 3 matrix A so that 0 0 1 3 0 0 0 0 1 A = 3 2 9 0 5 0 3 2 9 1 0 3 0 0 3 1 0 3 Do not compute this matrix product - it would only make your life harder H! a) Find three linearly...

Q:

Problems : 9,11,24,25,26 Direction : in the exercices 9 and 11 find a basis for the eigenspace corresponding to each listed eigenvalueHello can I have some help here please. Can you write on a sheet...

Q:

The method for constructing a Jordan basis in Example 8.52 is simplified due to the fact that each eigenvalue admits only one Jordan block. On the other hand, the method used in the proof of Theorem...

Q:

Can you please help me with number 12 and number 15. I have provided the math chapter it came from and the answer from the back of the book: Thank you so much and Best wishes! 5.7 Matrix Exponentials...

Q:

Suppose you are considering two mutual funds: Fund A and Fund B. Fund A has an expense ratio of 1.5% and an average annual return of 8%. Fund B has an expense ratio of 2% and an average annual return...

Q:

It is known by researchers that 1 in 100 people carry a gene that leads to the inheritance of a certain chronic disease. From a random sample of 1000 individuals, what is the probability that fewer...

Q:

What do the D-Day Survivors conclude about Company A's contributions to the attack? Company A made greater contributions than any other Company Company A made an average contribution Company A's...

Q:

2.10 Joanna is considering three possible jobs. The following table shows the possible incomes she might get in each job. Outcome A Outcome B Probability Earnings Probability Earnings Job 1 0.5 20...

Q:

Repeat the analyses in Problem 14.39, but account for covariate differences between groups?

Q:

What are the estimated incidence rates in the ASA and control groups? Cancer Suppose we wish to study the association between aspirin intake and the incidence of colon cancer. We find that 10% of...

Q:

What is a hazard rate in the context of this study? Pulmonary Disease A study was performed among 169,871 Chinese men and women in 1991 ages 40 years and older [13]. Baseline data were collected in...

Q:

It says "Mark owns a 20% interest in a partnership (not real estate) in which his at-risk amount is $44000 at the beginning of the year. During the year, the partnership borrows $90000 on a recoursw...

Q:

QUESTIONS Vrterest id or accrued during 2018 on regate quistion deteness of million or enim formare persone con is deductible wrate de interest QUESTIONS

Q:

Lupo Corporation uses a job-order costing system with a single plantwide predetermined overhead rate based on machine-hours. The company based its predetermined overhead rate for the current year on...