The method for constructing a Jordan basis in Example 8.52 is simplified due to the fact that each eigenvalue admits only one Jordan block. On the other hand, the method used in the proof of Theorem 8.51 is rather impractical Devise a general method for constructing a Jordan basis for an arbitrary matrix, paying careful attention to how the Jordan chains having the same eigenvalue are found.

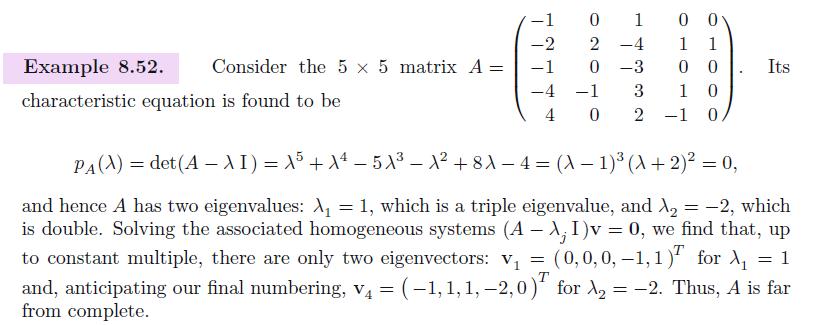
Theorem 8.51. 

Every n × n matrix admits a Jordan basis of Cⁿ. The first elements of the Jordan chains form a maximal set of linearly independent eigenvectors. Moreover, the number of generalized eigenvectors in the Jordan basis that belong to the Jordan chains associated with the eigenvalue λ is the same as the eigenvalue’s multiplicity.

Example 8.52. Consider the 5 x 5 matrix A = characteristic equation is found to be -1 -2 -1 -4 -1 4 01 00 2-4 1 1 00 3 1 0 0 2 -1 0 0 -3 Its PA(X) = det(A - X I) = A5 + A 5 A +8A - 4 = (A 1) (A + 2) = 0, and hence A has two eigenvalues: A = 1, which is a triple eigenvalue, and A = -2, which is double. Solving the associated homogeneous systems (A - X; I)v = 0, we find that, up to constant multiple, there are only two eigenvectors: v = (0,0,0,-1,1) for and, anticipating our final numbering, v = (-1,1, 1, -2,0) for A = -2. Thus, A is far from complete. = 1 V4