Consider Example 2. Build a model for Ace's decision and solve it both geometrically and algebraically.

Data from example 2

Again, consider Example 1 from Section 10.1. The following matrix represents the market share in percentages; the first number in each cell is Home Depot's share, and the second is Ace's share.

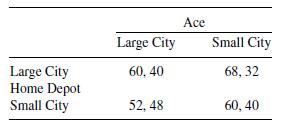
Home Depot wants to maximize its market share, as does Ace. The game is total conflict since the sum of the numbers in each cell is the constant 100. Thus, to maximize its share, Ace must minimize Home Depot's share—the only way for Ace to gain 1% is for Home Depot to lose 1%. For simplicity, we will consider only Home Depot's market share, with Home Depot maximizing its share and Ace minimizing Home Depot's share, much like the batter maximizing the average while the pitcher attempts to minimize the batter's average. When using a single set of values, we will use the row player's outcome values with the row player maximizing those values and the column player minimizing the row player's outcome values. Thus, we have the following game:

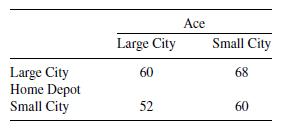
For Home Depot, we define the following variables:
S Percentage of market share. x Portion of the time to locate in a Large City. (1— x) Portion of the time to locate in a Small City If Ace plays a pure Large City (ALC) strategy, the expected value is:

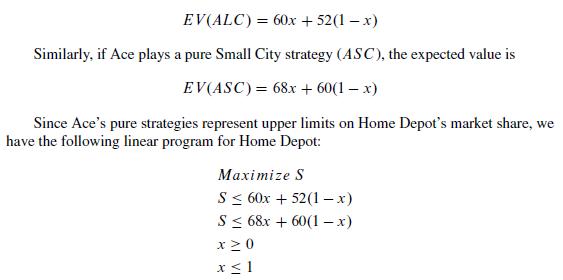
The linear program is solved geometrically in Figure 10.22, and the optimal solution is x = 1, which means Home Depot should always play its Large City strategy, and its market share is 60%.

Figure 10.22

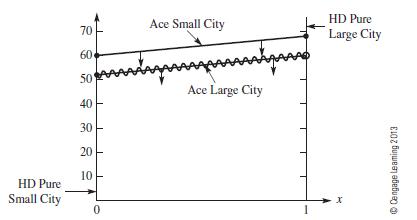
For the algebraic solution, there are only four intersection points in the interval 0≤ x≤ 1 as follows:

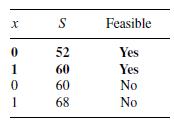
The analysis for Ace is similar and results in a pure strategy of Large City.