(a) Find the points of inflection of the curve of (1). (b) Considering Φ 2 () and...

(a) Find the points of inflection of the curve of (1).

(b) Considering Φ²(ˆž) and introducing polar coordinates in the double integral (a standard trick worth remembering), prove

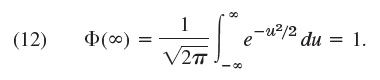
(c) Show that σ in (1) is indeed the standard deviation of the normal distribution. 

(d) Bernoulli€™s law of large numbers. In an experiment let an event A have probability p(0 < p < 1) and let X be the number of times A happens in n independent trials. Show that for any given ˆˆ > 0,

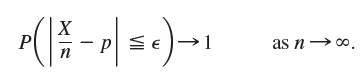
(e) If X is normal with mean μ and variance σ², show that X* = c₁X + c₂ (c₁ > 0) is normal with mean μ* = c₁μ + c₂ and variance σ*² = c²₁σ^2. 

Transcribed Image Text:

-и? (2 ди — du = 1. (12) Ф(с) %3D Ф(о) V2п +(E-|=-)-1 as n→ 00.