(a) Give reasons why Theorems 1 and 2 are more important than Theorem 3.

(b) Extend Theorem 1 by showing that if f(t) is continuous, except for an ordinary discontinuity (finite jump) at some t = α (>0) the other conditions remaining as in Theorem 1, then (see Fig. 117)

(1*) L(f') = sL(f) - f(0) - [f(α + 0) - f(α - 0)]e^-αs

(c) Verify (1*) for f(t) = e^-t if 0 < t < 1 and 0 if and 0 if t > 1.

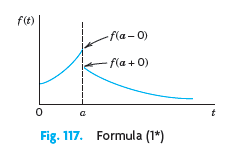
f(e) -f(a-0) f(a + 0) Formula (1*) Fig. 117.