(a) The Laplace transform of α piece wise continuous function f(t) with period p is Prove this theorem. Write « 0 = « p 0

(a) The Laplace transform of α piece wise continuous function f(t) with period p is

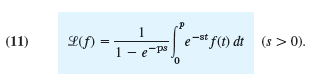
Prove this theorem. Write ˆ«^ˆž₀ = ˆ«^p₀ + ˆ«^2p_p + . . .. 

Set t = (n - 1)p in the nth integral. Take out e^-(n-1)p from under the integral sign. Use the sum formula for the geometric series.

(b) Using (11), show that the half-wave rectification of sin ωt in Fig. 137 has the Laplace transform

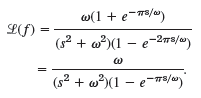
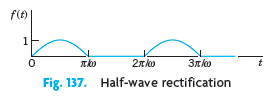
(A half-wave rectifier clips the negative portions of the curve. A full-wave rectifier converts them to positive; see Fig. 138.)

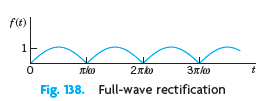
(c) Show that the Laplace transform of the full-wave rectification of sin ωt is

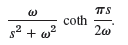
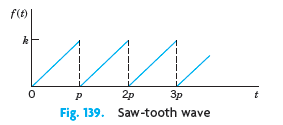
(d) Find the Laplace transform of the saw-tooth wave in Fig. 139.

(11) e-st f(t) dt (s > 0). L(f) 1- e-ps 0. w(1 + e-m/w) LF) (o? + w)(1 e-2ms/) (s + w?)(1 e-/)"