Following function is important in applied mathematics and physics (probability theory and statistics, thermodynamics, etc.) and fits
Question:
Following function is important in applied mathematics and physics (probability theory and statistics, thermodynamics, etc.) and fits our present discussion.
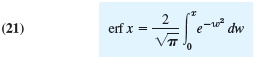
Regarding it as a typical case of a special function defined by an integral that cannot be evaluated as in elementary calculus, do the following.
Obtain the Maclaurin series of erf x from that of the integrand. Use that series to compute a table of erf x for x = 0(0.01)3 (meaning x = 0, 0.01, 0.02, · · ·, 3).
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
The error function erfx is defined as erfx 2 0x et2 dt We can expand the integrand in a Maclaurin se...View the full answer
Answered By
Brian Otieno
I'm Brian , an experienced professional freelancer with countless hours of success in freelancing many subjects in different disciplines. Specifically, I have handled many subjects and excelled in many disciplines. I have worked on many Computer Science projects and have been able to achieve a lot in that field. Additionally, I have handled other disciplines like History, Humanities, Social Sciences, Political science, Health care and life science, and Religion / Theology. My experience generally in these subjects has made me able to deliver high-quality projects in a very timely fashion. I am very reliable at my job and will get the work done in time, no matter what. In Addition, I have managed to ensure that the work meets my client's expectations and does not cause an error. I am a hard-working and diligent person who is highly responsible for everything I do. Generally, Freelancing has made me more accountable for doing my job. Additionally, I have had a passion for writing for the last seven years in this field.
0 Reviews
10+ Question Solved
Related Book For 
Question Posted:
