Question: Following function is important in applied mathematics and physics (probability theory and statistics, thermodynamics, etc.) and fits our present discussion. Regarding it as a typical

Following function is important in applied mathematics and physics (probability theory and statistics, thermodynamics, etc.) and fits our present discussion.

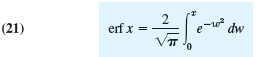
Following function is important in applied mathematics and physics (probability theory and

Regarding it as a typical case of a special function defined by an integral that cannot be evaluated as in elementary calculus, do the following.

It can be shown that erf (∞) = 1. Confirm this experimentally by computing erf x for large x.

Step by Step Solution

★★★★★

3.37 Rating (150 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

The error function erf is a special function that is widely used ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Advanced Engineering Mathematics Questions!

Following function is important in applied mathematics and physics (probability theory and statistics, thermodynamics, etc.) and fits our present discussion. Regarding it as a typical case of a...

Why the Monte Carlo Method is so important today Article ID Dirk P. Kroese The University of Queensland Tim Brereton Ulm University Thomas Taimre The University of Queensland Zdravko I. Botev The...

MATHEMATICS FOR MACHINE LEARNING Marc Peter Deisenroth A. Aldo Faisal Cheng Soon Ong Contents Foreword 1 Part I Mathematical Foundations 9 1 Introduction and Motivation 11 1.1 Finding Words for...

Applied Mathematics and Computation 95 (1998) 181192 Love dynamics: The case of linear couples Sergio Rinaldi 1 Centro Teoria dei Sistemi, CNR, Politecnico di Milano, Via Ponzio 34/5, 20133 Milan,...

Case Summary Read the Discussion Assignment 1-1 on p.24 of the text Winning and Longevity. Select a health care entity to focus on, this could be a clinic or hospital of your choosing. Apply the case...

SUMMARY this article for about 2 pages with single spacing. Thank you. ECONOMETRICS: MEASUREMENT I N ECONOMICS1 I As the first incumbent of a new Chair in this University, I thought that in this...

\fJournal of Mixed Methods Research http://mmr.sagepub.com Mixed Methods Sampling: A Typology With Examples Charles Teddlie and Fen Yu Journal of Mixed Methods Research 2007; 1; 77 DOI:...

Requirement: A two-page summary report on Board of Directors effectiveness based on the attached paper. Attributes and Structure of an Effective Board of Directors: A Theoretical Investigation...

A boiler operates at steady state. The entering water is a saturated liquid at P = 5 bar and has a flow rate of 10,000 kg/hr. The exiting steam is also at P = 5 bar and T = 400C. The pipe entering...

Classic Coverings (established in 2010) is in the process of updating its accounting policies for inventory costing, depreciation, and amortization. Decisions to implement a change on January 1,...

A production process produces electronic component parts. It is presumed that the probability of a defective part is 0.01. During a test of this presumption, 500 parts are sampled randomly and 15...

Develop a brief procedure or protocol (a simple list of points to be covered) for reviewing an employment application or rsum for possible inaccuracies or embellishments.

For a two-tailed test, if t ____ t cv , reject H 0 .

To calculate s M1M2 , one needs to know the sample ____ and the sample ____.

tra/courses/_551676_1/cl/outline G News Announcements - Grammarly Home My Ohio Po... Tenant Web Access... MyChart - F * Question Completion Status: Path Words:0 QUESTION 18 In the film you watched...

11 10 pts Market Analysis You are building a mixed-use development in a major city, located in a defined submarket. It will take two years to construct and begin leasing. The development will have a...

Harlan made equal payments at the end of each month into his RRSP. If interest in his account is 6.5% compounded annually, and the balance after eleven years is $14,500, what is the size of the...