Kutta€™s third-order method is defined by y_n+1= y_n+ 1/6(k₁+ 4k₂+ k^*₃) with k₁and k₂as in RK (Table 21.3) and k^*₃= hf(x_n+1, y_n- k₁+ 2k₂). Apply this method to (4) in (6). Choose h = 0.2 and do 5 steps. Compare with Table 21.5.

Table 21.3

Table 21.5

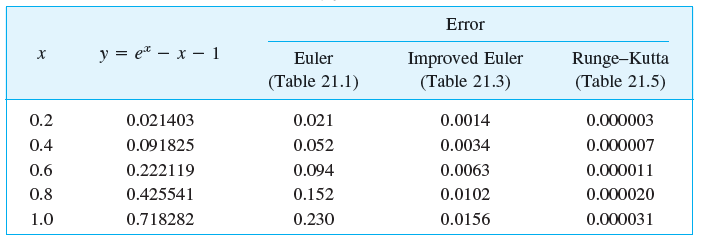
ALGORITHM RUNGE-KUTTA (f, xo, Yo, h, N). This algorithm computes the solution of the initial value problem y' = f(x, y), y(Xx) = Yo at equidistant points X1 = xo + h, x2 = xo + 2h, , XN = xo + Nh; (9) here f is such that this problem has a unique solution on the interval [Xo, Xx] (see Sec. 1.7). INPUT: Function f, initial values xo, Yo, step size h, number of steps N OUTPUT: Approximation yn+1 to the solution y(Xn+1) at xn+1 = xo + (n + 1)h, where n = 0, 1, , N 1 For n = 0, 1, .., N 1 do: ki = hf(xn, Yn) k2 = hf(xn + h, yn + k1) k3 = hf(xn + h, yn + k2) k4 = hf(Xn + h, yn + k3) Xn+1 = Xn + h Yn+1 = Yn + & (k1 + 2k2 + 2k3 + k4) OUTPUT xn+1 Yn+1 End Stop End RUNGE-KUTTA Error y = et x 1 Improved Euler (Table 21.3) Runge-Kutta (Table 21.5) Euler (Table 21.1) 0.000003 0.000007 0.000011 0.2 0.021403 0.091825 0.0014 0.021 0.052 0.094 0.152 0.4 0.0034 0.0063 0.0102 0.6 0.222119 0.425541 0.8 0.718282 0.230 0.0156 0.000020 0.000031 1.0