Let z n 1 z n curren q 1, so that the series z 1 z 2 middot middot middot converges by the ratio test Show that the remainder R n z n 1 z n 2 middot middot middot satisfies the inequality R n curren z n 1 (1 q) Using this, find how many terms suffice for computing the sum s of the series i 2 n 1

Question: Let |z n+1 /z n | ¤ q < 1, so that the series z 1 + z 2 + · · · converges by

Let |z_n+1/z_n| ‰¤ q < 1, so that the series z₁+ z₂+ · · · converges by the ratio test. Show that the remainder R_n= z_n+1+ z_n+2+ · · · satisfies the inequality |R_n| ‰¤ |z_n+1|/(1 - q). Using this, find how many terms suffice for computing the sum s of the series

:+ i п 2

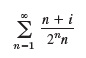
with an error not exceeding 0.05 and compute s to this accuracy.

:+ i 2"n -1

Step by Step Solution

★★★★★

3.45 Rating (174 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

The form of the estimate of R n suggests we use the fact that the r... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Advanced Engineering Mathematics Questions!

The financial statements of Tarbet Township contain the following data regarding financial position: Governmental fund balances $ 5,000,000 Capital assets used in governmental activities $2,375,000...

Show that Sup{| F n ( x , Ï) F ( x )|; x R1} For 0

Let X1, X2,..., Xn be a random sample from a uniform distribution on the interval [0, Ã¸], so that Then if Y = max (Xi), it can be shown that the rv U = Y/Ã¸ has density...

Let 0 ¤ Î³ ¤ a. Then a 100(1 - Î±)% CI for m when n is large is The choice Î³ = Î±/2 yields the usual interval derived in Section 7.2; if...

1.) Determine whether the series is absolutely convergent, conditionally convergent or divergent. (-1)"(6n) n=1 V16n4 - 1 Part 1: Test _ lanl The series _ lanl converges Justification: O A. By the...

1.) Determine whether the series is absolutely convergent, conditionally convergent or divergent. (-1)n-1 4vn n=1 7n + 1 Part 1: Test _ lanl The series _ lanl ? ? Justification: converges diverges O...

Show work/explanation where indicated. Answers without any work may earn little, if any, credit. You may type or write your work in your copy of the exam, or if you prefer, create a document...

Math 104A Homework #3 Instructor: Lihui Chai General Instructions: Please write your homework papers neatly. You need to turn in both full printouts of your codes and the appropriate runs you made....

1. It is possible to complete infinitely many tasks in a finite amount of time. 2. A series is the sum of the terms of a sequence. 3. Given the series _ an, then n is called the index of the series...

Donnie Smith Assignment Review for final due 05/02/2017 at 11:59pm MST 1. (1 point) Evaluate the indefinite integral. Z x4 p Sharma MAT 266 ONLINE B Spring 2017 5. (1 point) Find the slope of the...

I just need answers Do not care about the work just the answers Previous Problem Problem List Next Probiem m i: 9713 7 5712 + 13 (1 point) Use the limit comparison test to determine whether 2 an 2 d...

Repeat Problem 11.4, only set = 0.08. What is the lowest strike price at which early exercise will occur? What condition related to put-call parity is satisfied at this strike price? Discuss.

a. You plan to make five deposits of $1,000 each, one every 6 months, with the first payment being made in 6 months. You will then make no more deposits. If the bank pays 4% nominal interest,...

What are some techniques managers can use to maintain authority and structure without becoming overbearing and difficult to work with?

Sally Smith has an 80-year-old mother, Mary, who lives with her. Sally works full-time in the day and also attends to Marys needs. Sally still wants her mother to remain in her home with her;...

Assume that the power plant in Problem 9.45 has one closed FWH instead of the open FWH. The extraction flow out of the FWH is saturated liquid at 2033 kPa being dumped into the condenser, and the...

Investment Limited, a December 31 year-end publically traded company, reported income from continuing operations before taxes of $175,900 and pre-tax OCI of $36,000 in 2019. The OCI was entirely...

Water at 1000 kPa, 250C is brought to saturated vapor in a rigid container, shown in Fig. P6.51. Find the final T and the specific heat transfer in this isometric process. H2O FIGURE P6.51

Define the term multidisciplinary as it relates to hospital committees, and list at least three hospital committees.

Experimental avoidance usually requires (one/a few) _______________ conditioning trial(s), while phobic conditioning usually requires _______________ conditioning trial(s). Also,...

Refer to Exercise 13.77. a. What is the required condition to apply the t-test of two means to determine whether there is enough evidence to conclude that male heads of households (HHSEX: 1 = Male, 2...

Is there sufficient evidence that middle-class heads of households who work for someone else (OCCAT1: 1 = Someone else, 2 = Self employed/partnership) have higher incomes that heads of households who...

Refer to Exercise 13.79, which asked whether there is enough evidence to conclude that heads of households with college degrees (EDCL: 3 = some college, 4 = college degree) have more assets than...

1.Which of the following statements about price discrimination is TRUE? A .Price discrimination is a way for firms to extract some consumer surplus as an additional profit. B .Price discrimination...

Passive-voice verbs may be preferable in breaking bad news because they enable you to emphasize actions rather than personalities. Revise the following refusals so that they use instead of...

Suppose the returns on an asset are normally distributed. The historical average annual return for the asset was 5.7 percent and the standard deviation was 18.3 percent. What is the probability that...