Question: Obtain and in Prob. 52 from (22*) and (23***) and the original representation in Prob. 54 with parameter t. Data from Prob. 52
Obtain κ and τ in Prob. 52 from (22*) and (23***) and the original representation in Prob. 54 with parameter t.
Data from Prob. 52
Show that the helix [α cos t, α sin t, ct] can be represented by [α cos (s/K), α sin (s/K), cs/K], where K = √α2 + c2 and s is the arc length. Show that it has constant curvature k = α/K2 and torsion τ = c/K2.
Data from Prob. 54
Show that
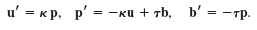
Step by Step Solution
3.49 Rating (176 Votes )
There are 3 Steps involved in it
From Prob 52 we know that the helix cos t sin t ct can be represented by cos sK sin sK c... View full answer

Get step-by-step solutions from verified subject matter experts


