Show that (a) Show that E(X - ) = 0, 2 = E(X 2 ) - 2 . (b) Prove (10)-(12). (c) Find

Show that

(a) Show that E(X - μ) = 0, σ² = E(X²) - μ².

(b) Prove (10)-(12).

(c) Find all the moments of the uniform distribution on an interval α ≤ x ≤ b.

(d) The skewness ϒ of a random variable X is defined by

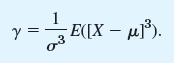
Show that for a symmetric distribution (whose third central moment exists) the skewness is zero.

(e) Find the skewness of the distribution with density f(x) = xe^-x when x > 0 and f(x) = 0 otherwise. Sketch f(x).

(f) Find a nonsymmetric discrete distribution with 3 possible values, mean 0, and skewness 0.

1 E([X pi).