Similarity is basic, for instance, in designing numeric methods.

(a) By definition, the trace of an n × n matrix A = [α_jk] is the sum of the diagonal entries,

trace A = α₁₁ + α₂₂ + · · · + Î±_nn.

Show that the trace equals the sum of the eigenvalues, each counted as often as its algebraic multiplicity indicates. Illustrate this with the matrices A in Probs. 1, 3, and 5.

Data from Prob. 1

Verify this for A and A = P^-1AP. If y is an eigenvector of P, show that x = py are eigenvectors of A. Show the details of your work.

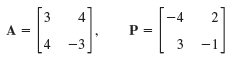
Data from Prob. 3

Verify this for A and A = P^-1AP. If y is an eigenvector of P, show that x = py are eigenvectors of A. Show the details of your work.

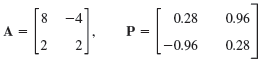
Data from Prob. 5

Verify this for A and A = P^-1AP. If y is an eigenvector of P, show that x = py are eigenvectors of A. Show the details of your work.

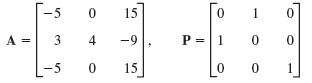
(b) Let B = [b_jk] be n × n. Show that similar matrices have equal traces, by first proving

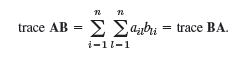
(c) Find a relationship between AÌ‚ in (4) and AÌ‚ = PAP^-1.

(d) What can you do in (5) if you want to change the order of the eigenvalues in D, for instance, interchange d₁₁ = λ₁ and d₂₂ = λ₂?

4 -4 2 A. 4 3 -3 -1 3. 0.28 P = 8. -4 0.96 [2 2 0.28 -0.96