If one attempted to dualize the notion of free module over a ring R (and called the object so defined "co-free") the definition would read: An R-module F is co-free on a set X if there exists a function _L: F → X such that for any R-module A and function ∫ : A → X, there exists a unique module homomorphism f̅ : A → F such that L∫= ∫(see Theorem 2.l(iv)). Show that for any set X with IXI ≥ 2 no such R-module F exists. If IXI = 1, then O is the only co-free module.

Data from theorem 2.1

Let R be a ring with identity. The following conditions on a unitary R-module F are equivalent:

(i) F has a nonempty basis;

(ii) F is the internal direct sum of a family of cyclic R-modules, each of which is isomorphic as a left R-module to R;

(iii) F is R-module isomorphic to a direct sum of copies of the left R-module R;

(iv) there exists a nonempty set X and a function L : X → F with the following property: given any unitary R-module A and function ∫: X → A, there exists a unique R-module homomorphism f̅ : F → A such that f̅_L = f. In other words, Fis a free object in the category of unitary R-modules. The theorem is proved below. A unitary module F over a ring R with identity, which satisfies the equivalent conditions of Theorem 2.1, is called a free R-module on the set X. By Theorem 2.1 (iv), F is a free object in the category of all unitary left R-modules. But such an F is not a free object in the category of all left R-modules (Exercise 15). By definition the zero module is the free module on the empty set. It is possible to define free modules in the category of all left R-modules over an arbitrary ring R (possibly without identity); see Exercise 2. Such a free module is not isomorphic to a direct sum of copies of R, even when R does have an identity (Exercise 2). In a few carefully noted instances below, certain results are also valid for these free modules in the category of all left R-modules. However, unless stated otherwise, the term "free module" will always mean a unitary free module in the sense of Theorem 2.1.

SKETCH OF PROOF OF 2.1.

(i) => (ii) Let X be a basis of F and x ϵ X. The map R→ Rx, given by r|→ x, is an R-module epimorphism by Theorem 1.5. If rx = 0, then r = 0 by linear independence, whence the map is a monomorphism and R ≅ Rx as left R-modules. Verify that F is the internal direct sum of the cyclic modules Rx (x ϵ X).

(ii)=> (iii) Theorem 1.15 and Exercise 1.8.

(iii) =} (i) Suppose 

and the copies of Rare indexed by a set X. For each x ϵ X let θ_x, be the element {r_i} of 

where r_i = 0 for i ≠ x and r_x = 1_R, Verify that {θ_x| x EX} is a basis of 

and use the isomorphism to obtain a basis of F. {i) => (iv) Let X be a basis of F and _L : X → F the inclusion map. Suppose we are 

given a map ∫ : X → A. If u ϵ F, then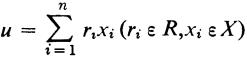 

since X spans F. If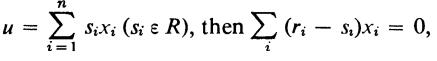 

whence r_i = s_i for every i by linear in dependence. Consequently, the map f̅ : F → A given by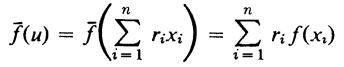 

is a well-defined function such that f̅_L = f Verify that ]is an R-module homomorphism. Since X generates F, any R-module homomorphism F →A is uniquely determined by its action on X. Thus, if g : F → A is an R-module homomorphism such that gL = ∫, then for every x ϵ X, g(x) = g(_L(x)) =∫(x) =f̅(x), whence g = f̅ and f̅ is unique. Therefore, by Definition 1.7.7 F is a free object on the set X in the category of unitary R-modules (iv) ⇒ (iii) Given L : X → F construct the direct sum 

with one copy of R for each x ϵ X. Let Y = { θ_x| x ϵ X| be the basis of the (unitary) R-module 

is a free object on the set Y in the category of R-modules 

Since IXI = I YI, the proof of Theorem I. 7 .8 implies that there is an R-module isomorphism 

such that f(,(X)) = Y.

REMARKS.

(a) If F is a free R-module on a set X(_t : X → F), then the proof of (iv) ⇒ (iii) of Theorem 2.1 implies that ,(X) is actually a basis of F.

(b) Conversely, the proof of (i) ⇒ (iv) of Theorem 2.1 shows that if X is a basis of a unitary module F over a ring R with identity, then F is free on X, with L : X → F the inclusion map.

(c) If X is any nonempty set and R is a ring with identity, then the proof of Theorem 2.1 shows how to construct a free R-module on the set X. Simply let F be the direct sum 

with the copies of R indexed by the set X. In the notation of the proof, { θ_x|x ϵ X| is a basis of F so that 

Since the map _l : X → F, given x|→ θ_x, is injective it follows easily that Fis free on X in the sense of condition (iv) of Theorem 2.1. In this situation we shall usually identify X with its image under _L, writing x in place of θ_x so that X ⊂ F. In this notation 

s written as 

and a typical element of F has the form r₁x₁ + · · · + r_nx_n (r_i ϵ R;x_i ϵ X). In particular, X = _L(X) is a basis of F.

(d) The existence of free modules on a given set in the category of all modules over an arbitrary ring (possibly without identity) is proved in Exercise 2.  

Transcribed Image Text:

F=ΣR