Let G be a finite abelian group and x an element of maximal order. Show that (x) is a direct summand of G. Use this to obtain another proof of Theorem 2.1.

Data from theorem 2.1

Every finitely generated abelian group G is (isomorphic to) a finite  direct sum of cyclic groups in which the finite cyclic summands (if any) are of orders  m1, ... ,mi, where m1 > 1 and m₁|m₂|· · ·|m_t.

Theorem 2.1.

If G ≠ 0 and G is generated by n elements, then there is a free abelian  group F of rank n and an epimorphism π : F → G by Theorem 1.4. If π is an isomorphism,  then G ≅ F ≅ Z⊕· · · ⊕Z (n summands). If not, then by Theorem 1.6  there is a basis { X₁, ... , X_n} of F and positive integers d₁, ... , d_r such that 1 ≤ r ≤ n, n  d₁|d₂|···|d_r, and {d₁x₁, ... , d_rx_r} is a basis of K = Ker π. Now 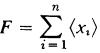and 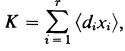where (x_i) ≅ Z and under the same isomorphism (d_i,x_i) ≅ d_iZ = {d_iu|u ϵ Z|. For i = r + 1, r + 2, ... , n let d_i = 0 so that 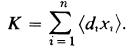Then by Corollaries 1.5. 7, 1.5.8, and 1.8.11 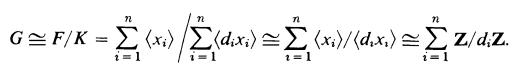If di= 1, then Z/diZ = Z/Z = 0; if d_i > 1, then Z/diZ ≅ Z_di; if d_i= 0, then Z/d_iZ = Z/0 ≅ Z. Let m₁, ... , m_t be those d_i, (in order) such that d_i ≠ 0, 1 and let s be the number of d, such that d_i = 0. Then

Transcribed Image Text:

72 F = Σ (x₂) i=1