Calculation of return ratio begins by breaking a feedback loop at a controlled source. However, breaking a feedback loop at a controlled source is often impossible in a SPICE simulation because the controlled source (e.g., the g_msource in a transistor€™s small-signal model) is embedded in a small-signal model. Therefore, it cannot be accessed or disconnected in simulation. A technique that can be used to simulate the return ratio with SPICE is illustrated in Fig. 8.60 for the circuit in Fig. 8.59. First, the independent source V_iis set to zero. Next, ac test signals v_tand i_tare injected into the loop at a convenient point (e.g., at the €œX€ in Fig. 8.59), creating two modified versions of the circuit as shown in Fig. 8.60a and 8.60b. Using Fig. 8.60a, calculate R€™_i= ˆ’i_m/i_d. Using Fig. 8.60b, calculate R€™_v= ˆ’v_m/v_d. The amplitudes of test signals it and v_tdo not affect R€™_ior R€™_v. Also, these ac test signals do not affect the dc operating point of the feedback circuit. The return ratio R for the controlled source is related to R€™_iand R'_vby¹⁰

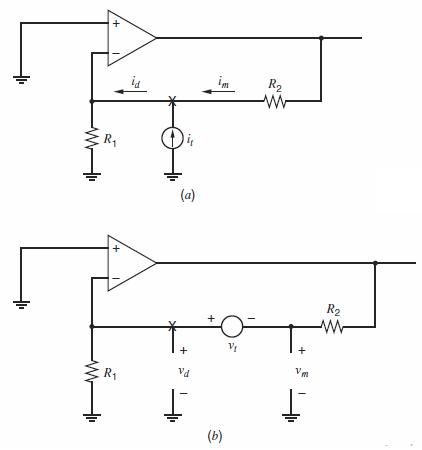
(a) Compute R€™_i and R€™_v for the circuit in Fig. 8.60. Use element values from Problem 8.32. Then combine these values using the equation above to find R.

(b) Compute R directly by breaking the loop at the a_v controlled source. Compare the results in (a) and (b).

(c) Carry out a SPICE simulation to find R€™_i and R€™_v. Then combine these values using the equation above to find R. Compare with your results from (a).

Fig. 8.59:

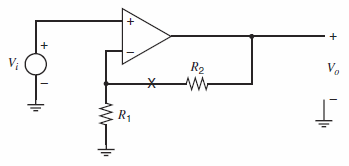
Fig. 8.60 (a) and (b):

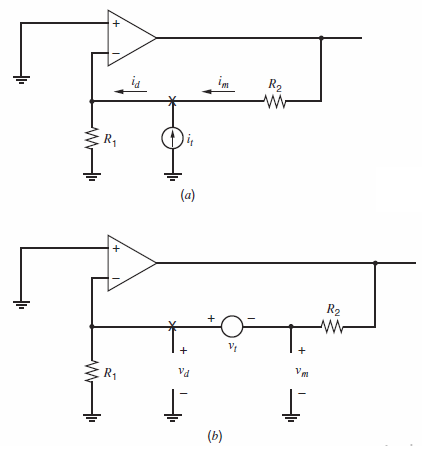
im R2 (a) R2 Vd R1 (b) V; R2 w- V. +,