Question: Present two examples in which successive repetitions of the NewtonRaphson algorithm do not approach a root. Apply the NewtonRaphson algorithm to the function f (x)

Present two examples in which successive repetitions of the Newton–Raphson algorithm do not approach a root. Apply the Newton–Raphson algorithm to the function f (x) = x^1/3 whose graph is drawn in Fig. 10(a). Use x₀ = 1.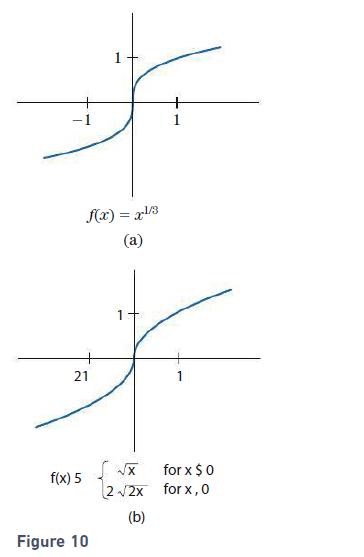 f(x) = x-/3 (a) 21 f(x) 5 Figure 10 1 2 2x

f(x) = x-/3 (a) 21 f(x) 5 Figure 10 1 2 2x (b) + 1 for x $ 0 for x,0

Step by Step Solution

★★★★★

3.47 Rating (173 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

The iterates d... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Applied Calculus Questions!

Use the Comparison Test or Limit Comparison Test to determine whether the following series converge. 1 3, k=1 k/2 + 1

Present two examples in which successive repetitions of the NewtonRaphson algorithm do not approach a root. Apply the NewtonRaphson algorithm to the function whose graph is drawn in Fig. 10(b). Use x...

The drawings show two examples in which a ray of light is refracted at the interface between two liquids. In each example the incident ray is in liquid A and strikes the interface at the same angle...

CANMNMM January of this year. (a) Each item will be held in a record. Describe all the data structures that must refer to these records to implement the required functionality. Describe all the...

answer the question clearly You are building a flight-control system for which a convincing safety case must be made. Would you assign the tasks of safety requirements engineering, test case...

(a) In SystemVerilog, what is the difference between: (i) The ternary operator ? and if...then...else statements? [2 marks] (ii) always_ff and always_comb? [2 marks] (iii) Blocking, non-blocking and...

ccn2 java solve them all . . . r2 e1 e2 box r2 Write sound typing and subtyping rules for these constructs. [5 marks] Now suppose that we add to this calculus the type variables and bounded universal...

ccm1 java attend all . . . r2 e1 e2 box r2 Write sound typing and subtyping rules for these constructs. [5 marks] Now suppose that we add to this calculus the type variables and bounded universal...

Demand and Supply Discussion Question: Applications-Ubereconomics Please read the article below and respond to the follow-up question: Why Uber Is an Economist's Dream Does 'surge pricing'...

Demand and Supply Discussion Question: Applications-Ubereconomics Please read the article below and respond to the follow-up question: Using Big Data to Estimate Consumer Surplus: The Case of Uber...

Use Logisim to construct a 32-bit ALU that performs all MIPS instructions.

Recall the Quimby case. This type of fraud is increasingly common. What could Quimby have done to protect himself?

Write a post describing a surgical procedure involving the digestive system, incorporting at least 1 5 relevant terms

Use the inverse transformation method to transform the following uniform variates U(2,4) to normal variates N(5,22) with mean of 5 and standard deviation of 2: u = {2.76,3.47,2.06,3.84}

The market research department of a soft drink manufacturer is investigating the effectiveness of a price discount coupon on the purchase of a two-liter beverage product. A sample of 5500 customers...

An article in the IEEE Transactions on Instrumentation and Measurement [Direct, Fast, and Accurate Measurement of V T and K of MOS Transistor Using VT-Sift Circuit (1991, Vol. 40, pp. 951955)]...

Consider the following data. Suppose that the relation - ship between Y and x is hypothesized to be Y = (Î² 0 + Î² 1 x + e) . 1 Fit an appropriate model to the data. Does the...

The following are partial income statement account balances taken from the December 31, 2021, year-end trial balance of White and Sons, Inc.: restructuring costs, $450,000; interest revenue, $55,000;...

Prepare an income statement for the company under i) Absorption costing Secure Home Fencing Sdn. Bhd. manufactures all types of security fencing with an extensive range of standard products, which...

taxation Prendy is employed to the Ria Investment Limited as a Branch manager. For the year 2017 he received a basic salary of $300,000 per month and travelling allowance of $25,000 per month. Prendy...