Consider the dilation equation (9.138) with c 0 = 0, c 1 = c 2 = 1, so (x) = (2x 1) +

Consider the dilation equation (9.138) with c₀ = 0, c₁ = c₂ = 1, so φ(x) = φ(2x − 1) + φ (2x − 2). Prove that ψ(x) = φ(x + 1) satisfies the Haar dilation equation (9.139). Generalize this result to prove that we can always, without loss of generality, assume that c₀ ≠ 0 in the general dilation equation (9.138).

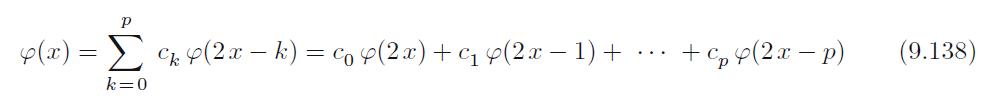
y(x) = (2x) + (2x 1). - (9.139)