Prove that a cubic B spline, as defined in Exercise 5.5.76, solves the dilation equation (9.138) for c₀ = c₄ = 1/8, c₁ = c₃ = 1/2, c₂ = 3/4.

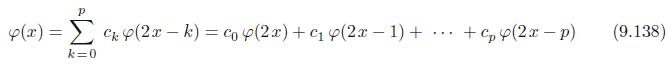
Data From Exercise 5.5.76

A bell-shaped or B-spline u = β(x) interpolates the data

(a) Find the explicit formula for the natural B-spline and plot its graph. 

(b) Show that β(x) also satisfies the homogeneous clamped boundary conditions u′(−2) = u′(2) = 0.

(c) Show that β(x) also satisfies the periodic boundary conditions. Thus, for this particular interpolation problem, the natural, clamped, and periodic splines happen to coincide.

(d) Show that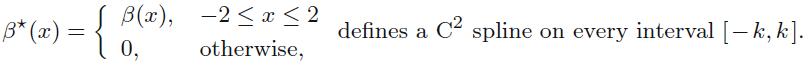 

() = P k=0 ekp(2x - k) = co(2x)+ (2r - 1) + ... + c(2x - p) (9.138)