Determine the spectrum for the trees in Exercise 2.6.9. Can you make any conjectures about the nature of the spectrum of a graph that is a tree?

Data From Exercise 2.6.9

A connected graph is called a tree if it has no circuits. 

(a) Find the incidence matrix for  each of the following directed trees:

(i)

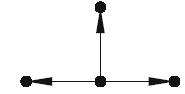
(ii)

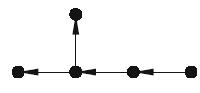
(iii)

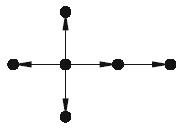
(iv)

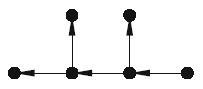
(b) Draw all distinct trees with 4 vertices. Assign a direction to the edges, and write down the corresponding incidence matrices. 

(c) Prove that a connected graph on n vertices is a tree if and only if it has precisely n − 1 edges.