Find the dual basis, as defined in Exercise 7.1.32, for the monomial basis of P⁽²⁾ with respect to the L² inner product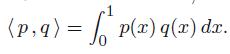

Data From Exercise 7.1.32

Dual Bases: Given a basis v₁, . . . , v_n of V, the dual basis ℓ₁, . . . , ℓ_n of V^∗ consists of  the linear functions uniquely defined by the requirements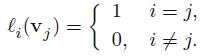 

(a) Show that ℓ_i[v] = x_i gives the i^th coordinate of a vector v = x₁v₁ + · · · + x_nv_n with respect to the given basis. 

(b) Prove that the dual basis is indeed a basis for the dual vector space. 

(c) Prove that if V = R_n and A = (v₁ v₂ . . . v_n) is the n × n matrix whose columns are the basis vectors, then the rows of the inverse matrix A⁻¹ can be identified as the corresponding dual basis of (R_n)^∗.

-1 (p, q): = [ p(x) q(x) dx. P