(i) Combine Exercises 10.1.23–24 to show that if A = SS⁻¹ is diagonalizable, then the solution to u̇ = Au can be written as u(t) = S (c₁ e^{λ1 t}, . . . , c_n e^{λn t})T, where λ₁, . . . , λ_n are its eigenvalues and S = (v₁ v₂ . . . v_n) is the corresponding matrix of eigenvectors.

Data From 10.1.23

Prove that the general solution to a linear system u̇ = Λu with diagonal coefficient a matrix Λ = diag (λ₁, . . . , λ_n) is given by u(t) = (c₁ e^λ1 t, . . . , c_n e^λnt)^T.

Data From 10.1.24

Show that if u(t) is a solution to u̇ = Au, and S is a constant, nonsingular matrix of the same size as A, then v(t) = Su(t) solves the linear system v̇ = Bv, where B = SAS⁻¹ is similar to A.(ii) Write the general solution to the systems in Exercise 10.1.13 in this form.

Data From Exercise 10.1.13

Solve the following initial value problems:

(a)

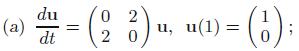
(b)

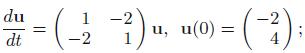
(c)

(d)

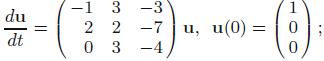
(e)

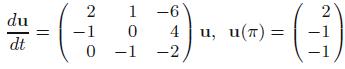
(f)

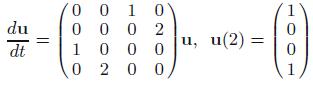
(g)

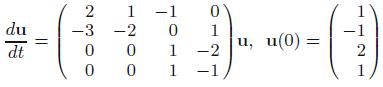
(a) du dt 02 20 u, u(1) = (6);