Question: Let A be a nonsingular square matrix. Prove the following formulas for its condition number: (a) (b) K(A) max{ || Au|| | || u ||

Let A be a nonsingular square matrix. Prove the following formulas for its condition number:


(a)


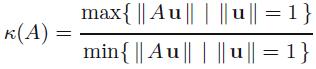
K(A) max{ || Au|| | || u || = 1} min{ ||


(b)


Au|| | ||u|| = 1)

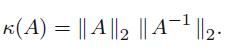
K(A) max{ || Au|| | || u || = 1} min{ || Au|| | ||u|| = 1)

Step by Step Solution

★★★★★

3.44 Rating (179 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

ANSWER a First we note that the condition number of a nonsingular square matrix A is defined as KA A ... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Applied Linear Algebra Questions!

Q:

Let A be a nonsingular square matrix. (a) Prove that the product of the singular values of A equals the absolute value of its determinant: 1 2 ... n = |det A|. (b) Does their sum equal the absolute...

Q:

Let A be a nonsingular 2 Ã 2 matrix with singular value decomposition A = P QT and singular values Ï1 ¥ Ï2 > 0. (a) Prove that the image of the unit (Euclidean) circle under the...

Q:

Prove that the condition number of a nonsingular matrix is given by k(A) = ||A||2 ||A-1||2.

Q:

CANMNMM January of this year. (a) Each item will be held in a record. Describe all the data structures that must refer to these records to implement the required functionality. Describe all the...

Q:

chapter 5 INTRODUCTION TO MATRIX ALGEBRA GOALS The purpose of this chapter is to introduce you to matrix algebra, which has many applications. You are already familiar with several algebras:...

Q:

chapter 5 INTRODUCTION TO MATRIX ALGEBRA GOALS The purpose of this chapter is to introduce you to matrix algebra, which has many applications. You are already familiar with several algebras:...

Q:

Math 400 Assignment #3 -- Numerical Integration and Differentiation 1. For the function g x e x 2 2 Due: 6am April 09, 2016 use the centered difference formula with h 101 , 102 , , 1020 to create a...

Q:

Could you please help with question 326? Thanks Exercise 309 Exercise 310 Theorem 3 Exercise 311 Exercise 312 75 5.8 Real symmetric matrices Real symmetric matrices play the role of real numbers in...

Q:

Could you please help with question 324 and 325? Thanks Exercise 309 Exercise 310 Theorem 3 Exercise 311 Exercise 312 75 5.8 Real symmetric matrices Real symmetric matrices play the role of real...

Q:

Could you please help with question 322 and 323? Thanks Exercise 309 Exercise 310 Theorem 3 Exercise 311 Exercise 312 75 5.8 Real symmetric matrices Real symmetric matrices play the role of real...

Q:

Why do we need to evaluate financial performance? How do you evaluate a company's financial health and performance? Provide two examples for each of the above.

Q:

Bazza's Bungy Jumping uses a different type and length of bungy cord depending on the weight of a customer. Bazza eyes-off a customer as they climb on to the jumping platform and classifies them as...

Q:

The Finance Director of MegaMart, Daniel Thompson, has encountered two complex accounting challenges that he is struggling to resolve. Given your expertise in intermediate financial accounting, he...

Q:

One of the major disadvantages of a sole proprietorship is the potential legal lia- bility. a. True b. False

Q:

Find the displacements u1, u2, ... u100 of 100 masses connected in a row by identical springs, with spring constant c = 1. Consider the following three types of force functions: (a) Constant force:...

Q:

(a) Suppose you are given three springs with respective stiffnesses c = 1. c = 2, c = 3. In what order should you connect them to three masses and a top support so that the bottom mass goes down the...

Q:

Generalizing Exercise 6.1.8. suppose you are given n different springs. (a) In which order should you connect them to n masses and a top support so that the bottom mass goes down the farthest under a...

Q:

Accounts Payable Accounts Receivable Accumulated Depreciation Building Administrative expenses Advertising incurred Advertising Payable Bank Loan Building Capital Cash Depreciation Drawings...

Q:

A manufactured product has the following information for June. Standard Actual Direct materials (5 lbs. @ $8 per lb.) 42,900 lbs. @ $8.10 per lb. Direct labor (3 hrs. @ $16 per hr.) 25,200 hrs. @...

Q:

The total contribution margin for the month under varlable costing is: Multple Choice $89,900 $25,500 $78,300 $23,000 Tracle Corporation manufactures and sells women's skirts. Each skirt (unit)...