Question: Prove that (9.147) implies (x l), (x m) = 0 for all l m. (4(x), 4(x m)) = 4(x) 4(x m) dx
Prove that (9.147) implies φ(x − l), φ(x − m) = 0 for all l ≠ m.
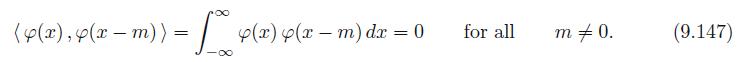
(4(x), 4(x m)) = 4(x) 4(x m) dx = 0 for all m = 0. (9.147)
Step by Step Solution
3.41 Rating (157 Votes )
There are 3 Steps involved in it
To prove that x l x m 0 for all l m we can use the fact that the Fourier transform of a Gaussian fun... View full answer

Get step-by-step solutions from verified subject matter experts


