Using the Euclidean norm, compute a fairly dense sample of points on the unit sphere S = {x R 3 | x = 1}.

Using the Euclidean norm, compute a fairly dense sample of points on the unit sphere S = {x ∈ R³ | ΙΙxΙΙ = 1}. 

(a) Set μ = .95 in (8.78), and then find the principal components of your data set. Do they indicate the two-dimensional nature of the sphere? If not, why not? 

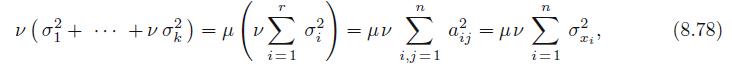
(b) Now look at the subset of your data that is within a distance r > 0 of the north pole, i.e., ΙΙx − ( 0, 0, 1 )^TΙΙ ≤ r, and compute its principal components. How small does r need to be to reveal the actual dimension of S? Interpret your calculations.

v(0+ +v6) = (2) = ; = - = i=1 i,j=1 n u i=1 19 (8.78)