Let x_i = (x_i, y_i), i = 1, . . . , m, be a set of data points in the plane. Suppose L^∗ ⊂ R² is the line that minimizes the sums of the squares of the distances from the data points to it, i.e., 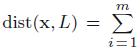dist(x_i, L), among all lines L ⊂ R². 

(a) Prove that x = (x, y) ∈ L^∗. 

(b) Use Exercise 8.8.11 to find L^∗.

Data From Exercise 8.8.11

Show that the first principal direction q₁ can be characterized as the direction of the line that minimizes the sums of the squares of its distances to the data points.

(c) Apply your result to the data points in Example 5.14 and compare the resulting line L^∗ with the least squares line that was found there.

dist (x, L) = i=1