Question: The trajectory of an object can be modeled as where y = height (m), 0 = initial angle (radians), x = horizontal distance (m),

The trajectory of an object can be modeled as

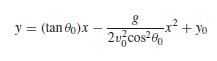
y = (tan60)x g 2ucos00 x + yo

where y = height (m), θ₀ = initial angle (radians), x = horizontal distance (m), g = gravitational acceleration (= 9.81 m/s²), v₀ = initial velocity (m/s), and y0 = initial height. Use MATLAB to find the trajectories for y₀ = 0 and ν₀ = 28 m/s for initial angles ranging from 15 to 75° in increments of 15°. Employ a range of horizontal distances from x = 0 to 80 m in increments of 5m. The results should be assembled in an array where the first dimension (rows) corresponds to the distances, and the second dimension (columns) corresponds to the different initial angles. Use this matrix to generate a single plot of the heights versus horizontal distances for each of the initial angles. Employ a legend to distinguish among the different cases, and scale the plot so that the minimum height is zero using the axis command.

y = (tan60)x g 2ucos00 x + yo

Step by Step Solution

★★★★★

3.39 Rating (161 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Here is an outline of the MATLAB code to solve the problem described Constants g 981 gravitational a... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Applied Numerical Methods Questions!

Use the following fact derived from Newton's Laws: An object released at an angle Î¸ with initial velocity v ft/s travels a horizontal distance A player located 18.1 ft from the basket...

The true weight of an object can be measured in a vacuum, where buoyant forces are absent. An object of volume V is weighed in air on a balance with the use of weights of density P. If the density of...

A zoom lens system is a combination of lenses that produces a variable magnification while maintaining fixed object and image positions. The magnification is varied by moving one or more lenses along...

Problem 4 : The trajectory of an object can be modeled as y = ( t a n 0 ) x - g 2 v 0 2 c o s 2 0 x 2 + y 0 where y = height ( m ) , 0 = initial angle ( radians ) , x = horizontal distance ( m ) , g...

3. The trajectory of an object can be modeled as 2v02 cos 2 where y height (m), 0o- initial angle (radians) x-horizontal distance (m) g gravitational acceleration-9.81 m/s), vo initial velocity (m/s)...

Problem 2.24 The trajectory of an object can be modeled as y= tan ) g_*+y 2 v cos2 where y = height (m), 0o= initial angle (radians), x = horizontal distance (m), g = gravitational acceleration (=...

The trajectory of an object can be modeled as - x + yo 8 y= (tan 20jcose, where y = height (m). 80 = initial angle (radians), x = horizontal distance (m), g = gravitational acceleration (= 9.81...

MATLAB 3. The trajectory of an object can be modeled as (tan ):-2002 where y height (m), 6- initial angle (radians) x horizontal distance (m) g gravitational acceleration(-9.81 m/s Vo initial...

(9%) Problem 7: Apollo 14 astronaut Alan B. Shepard Jr. used an improvised six-iron to strike two golf balls while on the Fra Mauro region of the moon's surface, making what some consider the longest...

2. The trajectory of an object can be modeled as y=tan(0)x2v02cos2(0)gx2+y0 where y= elevation (m),0= initial or launch angle (rad),x= horizontal distance or range (m),g= gravitational accelcration...

Express numbers as integers and simplify the below fractions. x=-(1)/(5)y+12 10x+2y=15

On January 1, 2019, Minas Company purchased a mining site in the mountains for the extraction of minerals. The site costed P12,500,000. Having no residual value, the mining site was annually...

Individual Tax Return - Henry Please use 2024 tax law. Required: Use the following information to complete Johnelle and Latoya Henry's 2024 federal income tax return. If any information is missing,...

2.3 Let X1, . . . ,Xn be a random sample from a population with distribution function F(x ), where F is symmetric, absolutely continuous, 0 , nondecreasing in each argument Xi, i = 1, . . . , n....

(a) Create a 3 x 3 Hilbert matrix. This will be your matrix [A]. Multiply the matrix by the column vector {x} = [1, 1, 1]T. The solution of [A] {x} will be another column vector {b}. Using any...

Perform the same calculations as in Example 11.1, but for the tridiagonalsystem, 0.8 -0.4 --0.4 0.8 --0.4 25 X2 0.8 -0.4 105

Determine the matrix inverse for Example 11.1 based on the LU decomposition and unit vectors.

Kolbys Korndogs is looking at a new sausage system with an installed cost of $514,000. This cost will be depreciated straight-line to zero over the projects four-year life, at the end of which the...

Five years ago, Big Dawg's Bones purchased a flivver for $373,986 that was depreciated straight-line to zero over 7 years. what is the current book value of the flivver? Five years ago, Big Dawg's...

A Swiss business just completed transactions in America and England. It is now holding $430,000 and 830,000 and wants to convert to Swiss francs and will use the following exchange rates. USD/SFR...