Use the fitted model from the previous exercise to compute the linear trend coefficient
\[
\frac{\sum t\left(\hat{\gamma}_{1}(t)-\hat{\gamma}_{0}(t)ight)}{\sum t^{2}}
\]
and its standard error. You should find both numbers in the range \(0.013-0.015\) per month, similar to, but not exactly the same as those reported in the text.

Data From previous exercise 

According to the text in Sect. 5.5, Virtual randomization requires the timezero average for feral hosts to be the same as that for giant runts, but the temporal trends are otherwise unconstrained. It appears that the model matrix spanning this subspace is not constructible using factorial model formulae. Explain how to construct the desired matrix including a constant additive sex effect. What is its rank? Fit the model as described in the text following Table 5.4. Include independent Brownian motions for aviaries and lineages, plus an additional baseline error term with independent and identically distributed components.

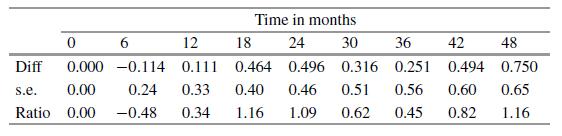
0 Diff 0.000 s.e. 0.00 Ratio 0.00 Time in months 24 6 12 18 -0.114 0.111 0.464 0.24 0.33 0.40 -0.48 0.34 1.16 30 36 42 48 0.496 0.316 0.251 0.494 0.750 0.46 0.51 0.56 0.60 0.65 1.09 0.62 0.45 0.82 1.16