Order Statistics. Let X₁, X₂, €¦. X_nbe a random sample of size n from X, a random variable having distribution function F(x). Rank the elements in order of increasing numerical magnitude, resulting in X₍₁₎, X₍₂₎,€¦, X_(n), where X₍₁₎is the smallest sample element (X₍₁₎= min{X₁, X₂,€¦, X_n}) and X_(n)is the largest sample element (X_(n)= max{X₁, X₂,€¦, X_n}). X_(i)is called the ith order statistic. Often the distribution of some of the order statistics is of interest, particularly the minimum and maximum sample values X₍₁₎and X_(n), respectively.

(a) Prove that the cumulative distribution functions of these two order statistics, denoted respectively by F_X(1) (t) and F_X(n) (t), are

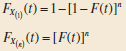
(b) Prove that if X is continuous with probability density function f (x), the probability distributions of X₍₁₎ and X_(n) are

(c) Let X₁, X₂,€¦, X_n be a random sample of a Bernoulli random variable with parameter p. Show that

(d) Let X₁, X₂,€¦, X_n be a random sample of a normal random variable with mean μ and variance σ². Derive the probability density functions of X₍₁₎ and X_(n). 

(e) Let X₁, X₂,€¦, X_n be a random sample of an exponential random variable of parameter λ. Derive the cumulative distribution functions and probability density functions for X₍₁₎ and X_(n).

Fx (1) =1-[1- F(t)r Fx, (t) = [F(t))* fx(1) = n[1 F(0)]" f) Sx,() = n[F()]*" f) %3D