You are given a model with two distinct label variables Y₁, Y₂, and there is a super label Z which conditions all of these labels, thus giving us this hierarchical na¨ıve Bayes model. The conditional probabilities for the model are parametrized by p₁, p₂, q₀, q₁ and r.

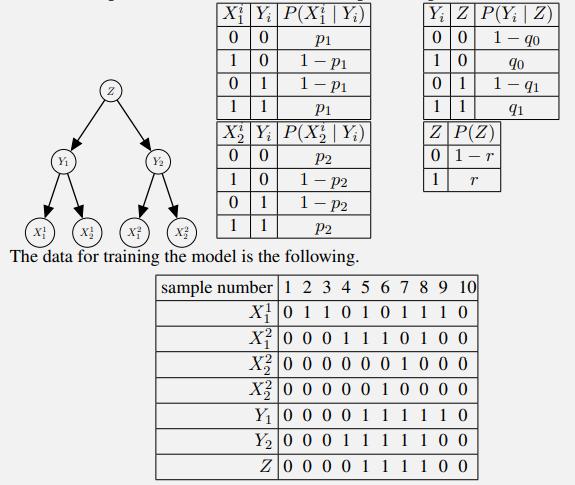a. Compute the maximum likelihood estimate of p₁, p₂, q₀, q₁ and r.

b. Now we are given a partial data point with X²₁ = 1, X²₂ = 1, Y₁ = 1. Find the probability that Y₂ = 1 in terms of the parameters p₁, p₂, q₀, q₁ and r (you might not need all of them).

Xi|Y|P(X|Y) 0 0 1 0 01 1 1 X Y P(X Y) 0 0 1 0 0 1 11 X (X (x X The data for training the model is the following. P1 1-P1 1-P1 P1 P2 1-P2 1-P2 P2 YZ P(Y,Z) 0 1-90 90 1-91 91 10 01 1 1 Z P(Z) 01-T 1 T sample number 1 2 3 4 5 6 7 8 9 10 X 0 1 1 0 1 0 1 1 1 0 X 0 0 0 1 1 1 0 1 0 0 X2 0 0 0 0 0 0 1 0 0 0 X2 0 0 0 0 0 1 0 0 0 0 Y 0 0 0 0 1 1 1 1 1 0 Y 0 0 0 1 1 1 1 1 0 0 Z 0 0 0 0 1 1 1 1 0 0