In Example 1, change 2cos to tan. Data from Example 1 Solve the equation 2 cos 1 = 0 for all values of

In Example 1, change 2cosθ to tanθ.

Data from Example 1

Solve the equation 2 cosθ − 1 = 0 for all values of θ such that 0 ≤ θ ≤ 2π. Solving the equation for cosθ, we obtain cosθ = 1/2. The problem asks for all values of θ from 0 to 2π that satisfy the equation. We know that the cosines of angles in the first and fourth quadrants are positive. Also, we know that cos π/3 = 1/2 which means that π/3 is the reference angle. Therefore, the solution proceeds as follows:

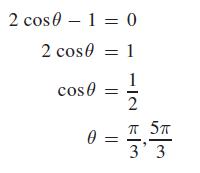
2 cos 0 - 1 = 0 2 cos = 1 cose 0 IN FIM 5 3 3